Александр Гурштейн - Извечные тайны неба

Биографы Ньютона соревновались в придумывании превосходных степеней в оценке его деятельности. Но вряд ли можно оценить ее проще и лучше, чем это сделал сам Ньютон незадолго до смерти: «Не знаю, чем я могу казаться миру, но сам себе я кажусь только мальчиком, играющим на морском, берегу, развлекающимся тем, что от поры до времени отыскиваю камешек более цветистый, чем обыкновенно, или красивую раковину, в то время как великий океан истины расстилается передо мной неисследованным».

В науке Ньютон, подобно Копернику, объединил разрозненные представления своих предшественников и, опираясь на плечи исполинов, создал общую физическую концепцию, заставив физику на протяжении последующих трехсот лет говорить его языком.

Подобно Копернику, Ньютон очень придирчиво относился к результатам своей научной работы. Если исследованиями проблемы тяготения Ньютон занимался в 1665-1667 гг., когда ему не исполнилось еще 25 лет, то опубликован закон всемирного тяготения был 20 лет спустя. Книга «Математические начала натуральной философии», принесшая ее автору славу одного из величайших ученых всех времен, вышла в свет лишь в 1687 г., когда Ньютону было уже 45 лет.

Так же как и у Коперника, у Ньютона был свой «добрый гений», – молодой, полный энтузиазма помощник, который всеми силами способствовал завершению и публикации труда своего великого соотечественника. Это был блестящий астроном Эдмонд Галлей, известный в астрономии несколькими важными открытиями. В частности, он открыл собственные движения «неподвижных» звезд и периодичность возвращения к Земле кометы, получившей впоследствии его имя.

Человек в высшей степени разносторонний, Галлей был создателем таблиц страхования жизни, редактировал классические тексты и отыскал место высадки в Британии Юлия Цезаря. На 65-м году жизни он был назначен королевским астрономом и не испугался избрать своей первой целью позиционные наблюдения Луны в течение 18-летнего цикла обращения узлов лунной орбиты. Эти наблюдения он и довел в действительности до конца. Таким был тот, кто убедил Ньютона издать свой труд и взял на себя его редактирование.

Из-за отсутствия у Королевского общества денег Галлей отдал на издание книги Ньютона собственные сбережения. Он был вовсе небогат и получил от Королевского общества в порядке возмещения затрат сначала 50 экземпляров книги «История рыб», а потом еще 20 экземпляров той же книги.

Закон всемирного тяготения нашел признание далеко не сразу, особенно на континенте. История признания этого закона – история геодезических измерений размеров Земли. Выводя одно из следствий закона всемирного тяготения, Ньютон рассуждал примерно следующим образом.

Вообразим, что в теле Земли прорыты две глубочайшие шахты, которые доходят до центра Земли и там соединяются (см. рисунок). Одна шахта прорыта строго вдоль оси вращения Земли, а другая, перпендикулярная к ней, – строго в плоскости экватора. Если такие шахты заполнить водой, то она сможет переливаться из одной шахты в другую и в конце концов займет положение, соответствующее фигуре равновесия.

Если бы Земля не вращалась вокруг оси, на воду в шахтах действовали бы совершенно одинаковые силы тяготения, и в обеих шахтах ее уровень установился бы на одинаковом расстоянии от центра. Фигура равновесия имела бы в этом случае форму шара.

Однако Земля не неподвижна, она вращается вокруг своей оси. При этом вода в экваториальной шахте приобретает центростремительное ускорение. За счет этого давление воды на дно в экваториальной шахте меньше, чем в осевой шахте. Понятно, что равновесие наступит лишь в том случае, когда в экваториальной шахте уровень воды повысится.

Таким образом, закончил свои рассуждения Ньютон, Земля, представляющая собой фигуру равновесия, должна иметь утолщение на экваторе или, что то же, быть сплюснутой у полюсов.

Приведенные рассуждения Ньютона показывают, что он впервые рассмотрел поверхность Земли как поверхность фигуры равновесия. При этом он предполагал, что плотность всех частей Земли одинакова, т. е. Земля является телом однородным. Считая Землю состоящей из бесконечного множества отдельных частичек, он, как это следует из закона всемирного тяготения, полагал, что каждая частичка притягивает к себе все остальные и в свою очередь притягивается ими. Из теоретических расчетов на основе сделанных предпосылок следовало, что расстояние от центра Земли до полюса должно быть на 0,43 % (около 28 км) короче расстояния от центра до экватора.

Теоретический вывод Ньютона оспаривался многими его современниками, которые считали, что Земля в целом либо имеет форму правильного шара, либо не сжата, а, напротив, вытянута у полюсов и имеет форму яйца. «Oblatum sive oblongum» – «сжатая или вытянутая» – вот спор, который оказался в центре внимания науки на рубеже XVII и XVIII вв. Решить этот спор могли только астрономы и геодезисты.

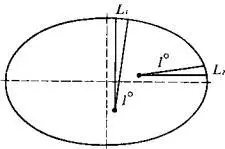
Если Ньютон прав, то сечение Земли по меридиану должно иметь форму эллипса. Конечно, земной эллипс сжат очень немного, гораздо меньше, чем это показано на рисунке. Но для того, чтобы лучше понять последующие рассуждения, использован эллипс с сильно преувеличенным сжатием.

Итак, пусть сечение Земли по меридиану имеет, согласно Ньютону, форму эллипса. Тогда дуги, соответствующие разности широт в 1°, в разных частях эллипса уже не будут равны между собой. На рисунке хорошо видно, что для эллипса, сжатого у полюсов, полярная дуга должна быть немного длиннее, чем экваториальная. Если бы Земля имела форму яйца, то сечение по меридиану тоже имело бы форму эллипса, но в этом случае полярная дуга оказалась бы короче экваториальной.

Таким образом, перед геодезистами встала ясно сформулированная задача. Необходимо с максимальной точностью измерить две дуги меридиана: одну на севере, ближе к полюсу, другую на юге, ближе к экватору, после чего сравнить их. В случае, если полярная дуга окажется длиннее экваториальной, прав Ньютон. Если же полярная дуга окажется короче, то правы его противники: Земля имеет форму яйца.