Александр Гурштейн - Извечные тайны неба

Точные измерения протяженных расстояний по пересеченной местности всегда вызывали большие трудности и не могли выполняться с требуемой точностью. Удачный метод измерения больших расстояний удалось дать примерно за полвека до описываемых событий, в 1614 г., голландскому астроному и математику Снеллиусу, предложившему пользоваться для этой цели цепочками треугольников. Слово «треугольник» звучит по-латыни как «триангулум», а поэтому метод Снеллиуса получил название триангуляции.

Математические основы триангуляции крайне просты. Всякий плоский треугольник, как известно, состоит из шести элементов: трех сторон и трех углов. Если в треугольнике даны одна сторона и два угла, то такой треугольник можно «решить», т. е. исходя из известных элементов с помощью определенных формул вычислить величины неизвестных элементов. То же самое относится и к так называемым сферическим треугольникам, т. е. треугольникам, построенным на поверхности шара. Отсюда нетрудно понять существо метода триангуляции.

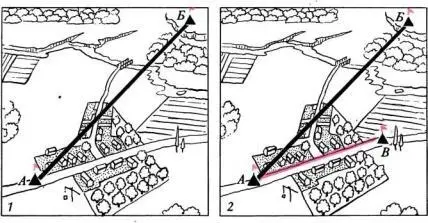
Пусть необходимо измерить расстояние между флажками, поставленными в точках А и Б (см. рисунок). Чтобы выполнить такое измерение непосредственно, потребовалось бы снести значительную часть домов, вырубить в лесу просеку, засыпать овраг и построить мост через реку. Стоимость всех этих работ выразится огромной суммой. На их выполнение уйдет немало времени.

Применение метода триангуляции позволяет обойти эти трудности. Поставим на дороге в точке В еще один флажок и измерим с максимально возможной точностью линию АВ. Дорога на этом участке прямая, ровная, и поэтому измерение может быть выполнено легко. Назовем измеренную линию базисом.

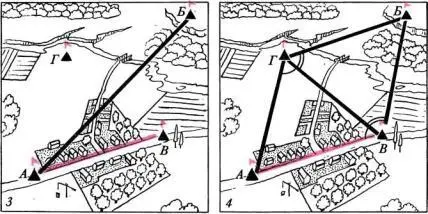
Обследовав местность, отметим флажком еще одну точку Г так, чтобы с нее были хорошо видны флажки в точках А, Б и В. Теперь пункты А, В и Г образуют на поверхности Земли треугольник, в котором сторона АВ известна. Остается измерить два угла, например в точках В и Г, после чего, решив треугольник, можно получить длины сторон АГ и ВГ и величину угла в точке А. Получив длину стороны ВГ, будем действовать дальше и измерим в точках В и Г два угла треугольника ВГБ. Зная длину стороны ВГ и значения углов в точках В и Г, отмеченные на рисунке двойной дужкой, вычислим длины сторон ВБ и ГБ и величину угла в точке Б. Таким образом, на поверхности Земли будут построены два треугольника АВГ и ВГБ, в которых известны все углы и все стороны. Теперь вычислим искомое расстояние АБ и поставленная задача разрешена.

Основное достоинство триангуляции заключается в том, что она сокращает до минимума дорогостоящие и исключительно трудоемкие линейные измерения. Они сводятся лишь к определению длины базиса, причем базис может быть выбран там, где его легче всего измерить. Наибольший объем работ в триангуляции составляют не линейные, а угловые измерения, выполнение которых сопряжено с гораздо меньшими трудностями. Для угловых измерений не имеет существенного значения, течет ли между пунктами река, растет ли кустарник или расположен глубокий овраг. Важно только, чтобы из одного пункта можно было беспрепятственно видеть другой. А этого, как правило, всегда можно добиться, если заранее намечать пункты на основе подробного знакомства с местностью.

Цепочки, состоящие из многих треугольников, позволяют с очень высокой точностью измерять на поверхности Земли расстояния в сотни и тысячи километров. В вершинах треугольников строят специальные геодезические знаки – вышки, благодаря которым стороны каждого из измеряемых треугольников могут достигать 20-30 км. В прежнее же время в качестве пунктов триангуляции использовались крепостные башни, колокольни и другие стоящие на высоких местах заметные сооружения.

Под руководством директора Парижской обсерватории Джана Доменика Кассини большие триангуляционные работы еще при жизни Ньютона выполнялись во Франции вдоль Парижского меридиана. Но эти измерения, затянувшиеся на долгие годы, так и не разрешили ожесточенного спора о форме нашей планеты. Кассини до самой смерти оставался яростным противником «сплюснутой» Земли. Той же ошибочной точки зрения придерживался и унаследовавший пост директора Парижской обсерватории Кассини-сын.

Окончательно вопрос о форме Земли был решен только в результате триангуляционных измерений двух дуг, расположенных в таких местах, где разность длин одного градуса меридиана наиболее заметна: одной – вблизи экватора и другой – по возможности близкой к полюсу.

Весной 1735 г. фрегат, на борту которого находились французские академики Бугер, Кондамин, Годен и их помощники, взял курс на Перу. А через год, в 1736 г., Францию покидали академики Мопертюи, Клеро, Камюз, Лемонье и шведский физик Цельсий. Их путь лежал на север в далекую, занесенную снегом Лапландию. Там, на границе Швеции и Финляндии, в долине реки Торнео должна была измеряться северная дуга.

Подробное описание работы этих двух экспедиций, навсегда вошедших в историю науки, читается как захватывающая повесть. Нестерпимая жара перуанских Кордильер, тропические ливни, лихорадка и нападения индейцев – вот с чем столкнулась экспедиция Бугера. Непроходимые болота, сырой промозглый туман и лютая стужа выпали на долю экспедиции Мопертюи.

Первой закончила свою работу северная экспедиция. И уже сравнения ее результатов с результатами прежних измерений на территории Франции оказалось достаточным, чтобы доказать реальность сжатия Земли у полюсов.

Вернувшийся в Париж в меховой, невиданной французами лапландской шапке Мопертюи был принят как национальный герой. Это был тот самый человек, который, по выражению Вольтера, «приплюснул Землю и всех Кассини». В честь Мопертюи была выбита золотая медаль, на которой он изображен в этой шапке, закутанный в меха, с палицей Геркулеса в одной руке и сплюснутой Землей в другой.

Впрочем, вскоре, поссорившись с Мопертюи, тот же острослов Вольтер не преминул кольнуть его язвительной эпиграммой:

Полувековой труд французских академиков окончательно доказал, что форма Земли, согласно Ньютону, соответствует фигуре, которая получается путем вращения эллипса вокруг его малой оси. Такая фигура называется в геометрии эллипсоидом вращения, или же просто двухосным эллипсоидом.