Екатерина Вавилова - Все науки. №6, 2022. Международный научный журнал

Ключевые слова:водный поток, напор, ускорение, скорость свободного падения.

Annotation.Large hydropower plants most often use the original design of creating platinum to increase the pressure of the incoming liquid, which leads to an increase in the total energy output. The article considers a theoretical assumption about the use of such a method of increasing the velocity of the flow itself using the properties of an ideal fluid from Bernoulli’s law and Torricelli’s formula.

Keywords:water flow, pressure, acceleration, free fall velocity.

Для больших гидроэнергетических установок часто преобладающими являются технологии создания плотин, где вода приводиться в близкое к статичному по отношению к общему объёму состоянию, после чего вода пропускается в канал, расположенный максимально низко под уровнем воды. Наличие такого ввода жидкости позволяет придавать массе дополнительную скорость благодаря потенциальной энергии, которая превращается в кинетическую.

Доказательством этого утверждения следует соотношение (1), из которого можно вывести как потенциальную энергию (2), так и кинетическую (3), далее при их равенстве (4), можно сделать вывод для скорости (5).

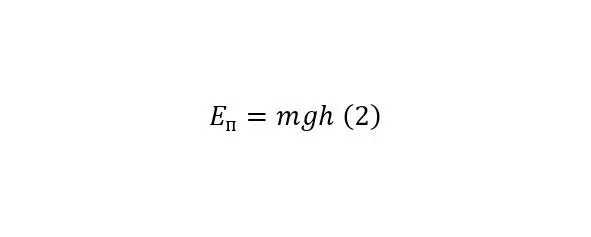
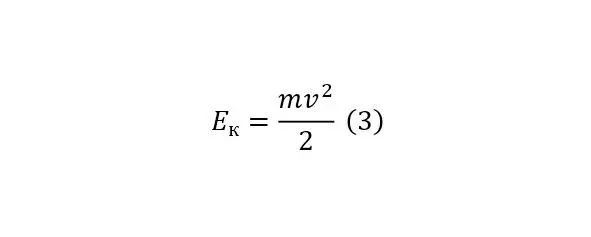
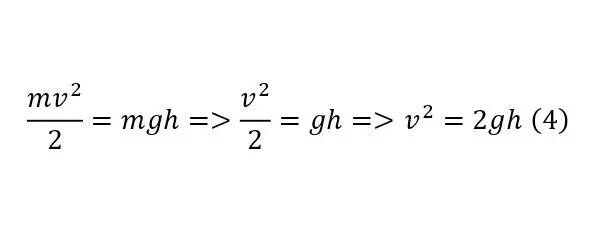
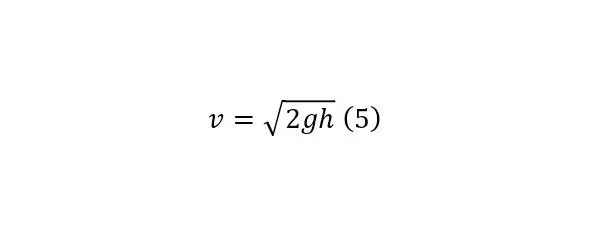
Но, чтобы указать на отношение этого вывода не только к обычным телам с высокой плотностью, то есть к твёрдым, но и к жидкостям, достаточно привести формулу Бернулли (6), вполне справедливую для жидкостей и вывод из неё этой же формулы (7—8).

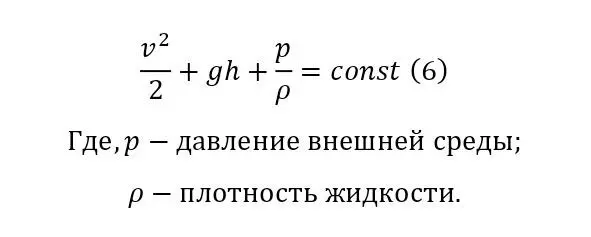
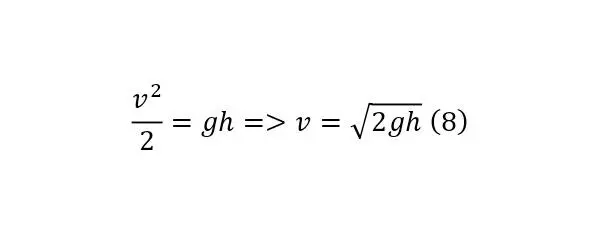
Из этого видна возможность получения вторичного дополнительного вектора, который чаще всего преобладает и заставляет двигаться именно под давлением самой воды, а вектор скорости притока в само водохранилище чаще всего гасится. Но когда же дело обстоит с обычными малыми гидроэнергетическими установками, здесь ситуация обстоит по-другому, поскольку тормозная способность имеющегося малого объёма в «плотине» не так высока и определяется по коэффициенту трения воды о воду, если так можно выразиться. То есть каждый отрезок, уменьшение происходит именно на указанный коэффициент энергии (9).

Данный вектор скорости суммируется с образующимся вектором скорости из-за давления (8) под прямым углом образуя результирующий вектор (10).

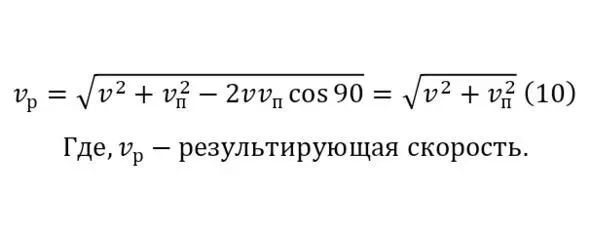
Выводимый результирующий вектор логично будет больше изначального вектора скорости (11), благодаря чему можно сделать вывод того, что использование плотин в конструировании малых гидроэнергетических установок вполне целесообразная технология.

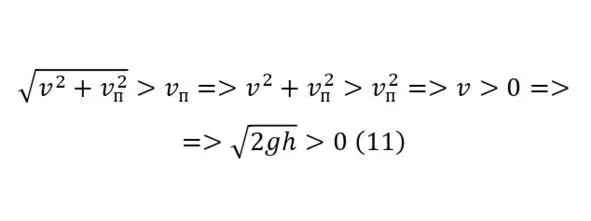
То есть какой бы ни была малой высота плотины и её разность между отверстием вывода потока и уровнем воды, действие, хоть и незначительное будет оказываться. Интересно здесь также и определение зависимости самой изначальной скорости и результирующего вектора (12).

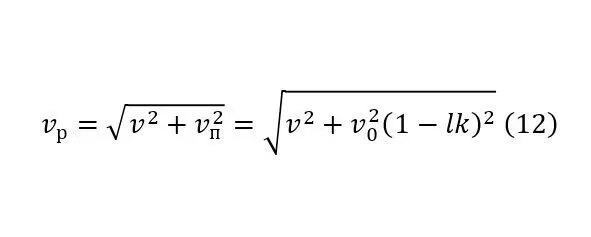
Эта зависимость была выведена, поскольку даже сама начальная скорость не совсем проста и за счёт того, что нижняя полость оврага для «водохранилища» должна быть выполнена в форме склона. Наряду с уменьшением по коэффициенту в зависимости от длины этого пути по (9), начальная скорость будет увеличиваться, поскольку к первоначальной скорости до входа в «водохранилище», при котором поток имел потенциальную энергию, кинетическая энергия, в которую превращается эта потенциальная, то есть действует тот же принцип (1—5), но при этом действует угловой коэффициент.

И если поскольку опять же этот потенциальный вектор направляющий вниз также находится под углом 90 градусов к основному первоначальному вектору, их суммированных вектор будет определяться по (13), создавая зависимость для начальной скорости от первоначальной в следующем расположении.

Откуда справедливо (14).

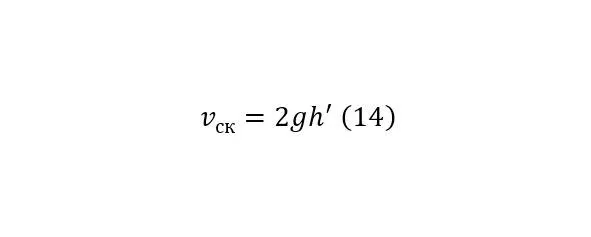
И важно учесть, что (13) вместе с (14) действует только при плоском склоне самого оврага, не считая коэффициент трения, в случае его расчёта в (14) включается дополнительный коэффициент, ровно, как и в иных случаях, для реализации, но этот коэффициент определяется эмпирически.

При действии же (13) и (14), ранее описанная (12) изменяется как (15).

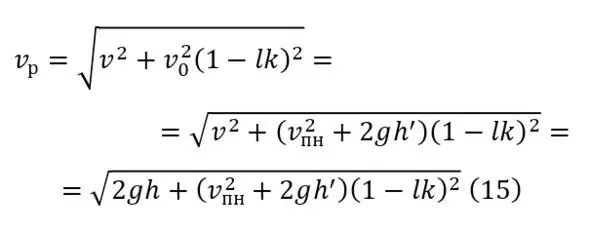
Таким образом (15) можно считать полноценной формулой при действии прямого склона на дне оврага. При наличии же нескольких векторов, целесообразно использование (16), по той простой причине, что несколько векторов не будут приходить из одного направления, ибо тогда их можно будет объединить в один. А разными вектора могут быть из-за наличия дополнительных поворотов, больших неровностей и подобных не существенных причин.

Заключительным штрихом служит лишь введение коэффициентов, о которых говорилось ранее, а именно о коэффициентах своего рода вязкости (18), зависящий от коэффициента сопротивления движения в потоке (17).

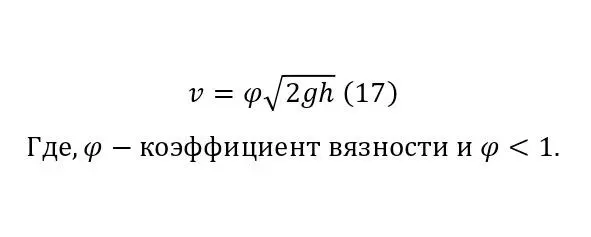
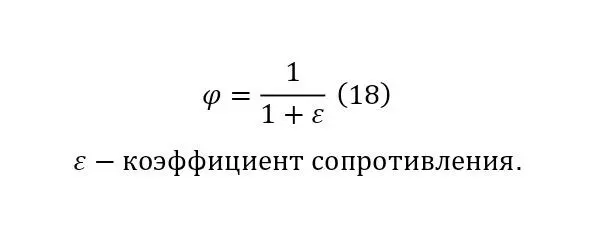
Такой вид (17) формулы (8) был доказан и описан итальянским учёным Эванджелиста Торричелли в 1643 году, а позже уже было показано, что эта формула, как уже упоминалось следствие закона Бернулли.