Герман Ефремов - Макрокинетика сушки
- Название:Макрокинетика сушки
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:2022
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Герман Ефремов - Макрокинетика сушки краткое содержание
Макрокинетика сушки - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Динамическое подобие описывается соотношениями сходственных сил, энергий и масс для модели и объекта, причем динамическое подобие может иметь место только при наличии подобия геометрического и кинетического.
1.11 Подобное преобразование дифференциальных уравнений переноса
Перенос количества движения. Рассмотрим динамическое подобие на примере подобного преобразования уравнения Навье-Стокса (1.10) для одномерного потока (перенос количества движения). В этом случае скорость потока 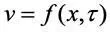 .
.
Запишем это уравнение для объекта:
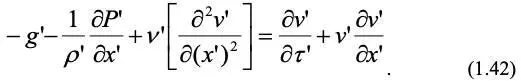
Аналогичное уравнение с учетом констант подобия запишем для модели:
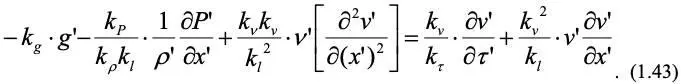
Чтобы уравнения (1.42) и (1.43) были идентичны, все множители из констант подобия должны быть равны, тогда:
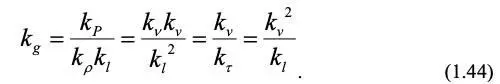
Домножив все члены уравнения (1.44) на kl /kv2, получим безразмерные соотношения:
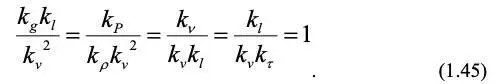
Эти соотношения после подстановки констант подобия дают выражения соответствующих критериев подобия Фруда, Эйлера, Рейнольдса и гомохнонности. Так для критерия Фруда .
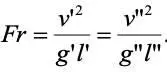
Опуская индексы, получим аналогично и другие критерии:
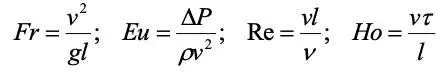
.
Для обеспечения подобия критерии подобия для объекта и модели должны быть численно одинаковы. Это положение определяет содержание 1-й теоремы подобия.
Так как члены уравнения Навье-Стокса представляют собой сумму удельных сил тяжести, давления, вязкости и инерции, то сравнивая их с выражениями критериев, можно сделать вывод, что критерий Фруда представляет собой отношение силы инерции к силе тяжести, критерий Эйлера – отношение силы давления к силе инерции, критерий Рейнольдса – отношение силы инерции к силе вязкости (учитывает режим движения) и критерий гомохронности – отношение инерционных сил модели и объекта (учитывает нестационарность процесса).
Обычно критерий Эйлера является определяющим и математическое описание явления переноса количества движения в критериальном виде с учетом геометрического критерия Г имеет вид:
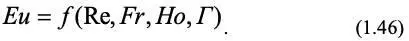
Таким образом, решение дифференциальных уравнений описывающих процесс можно представить в виде зависимостями между критериями подобия. Это положение известно как 2-я теорема подобия.
Выше было сказано, что для обеспечения подобия критерии подобия для объекта и модели должны быть численно равны, но тогда согласно зависимости (1.46) и определяющие критерии должны быть равны. Таким образом, для обеспечения подобия достаточно равенства определяющих критериев модели и объекта. Это положение определяет содержание 3-й теоремы подобия.
Положения, устанавливаемые тремя теоремами подобия, справедливы для любого вида переноса. Они используются как для постановки экспериментов, так и для математической их обработки.
Теплоперенос.Критерии теплопереноса выводятся аналогично выводу критериев переноса количества движения. Рассмотрим подобное преобразование уравнения Фурье-Кирхгофа (1.27) для одномерного теплопереноса, когда t = f ( x , τ) в отсутствии источников тепла для объекта моделирования (индексы опустим):
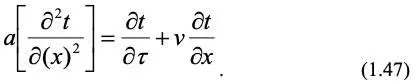
Аналогичное уравнение с учетом констант подобия запишем для модели:
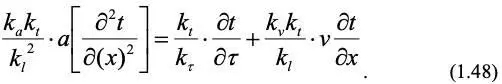
Чтобы уравнения (1.47) и (1.48) были идентичны, все множители из констант подобия должны быть равны, тогда:
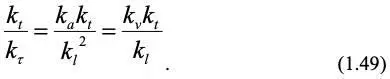
Из первого равенства выражения (1.49), подставив значения констант подобия, получим безразмерный комплекс – критерий Фурье, который характеризует изменение теплопереноса теплопроводностью во времени:

Из второго равенства выражения (1.49), подставив значения констант подобия, получим другой безразмерный комплекс – критерий Пекле, который представляет собой отношение теплопереноса за счет движения среды (конвективный) и за счет теплопроводности (молекулярный):
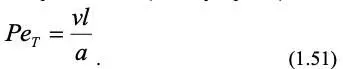
Он аналогичен по форме критерию Рейнольдса, который может быть рассмотрен как отношение скоростей переноса количества движения конвективного и молекулярного.
Поскольку на конвективный теплоперенос влияют условия движения среды и описывающие его дифференциальные уравнения решаются совместно с уравнениями движения потока, в критериальную зависимость, описывающую теплоперенос, должны входить и критерии гидродинамического подобия. Это критерии. Но, Fr, Re и Г . Критерий Эйлера обычно не входит в эту зависимость, т. к. не является определяющим для теплопереноса.
Так как в критерии Fr и Re входит скорость, используется их комбинация – критерий Галилея, не содержащий скорости:

или критерий Архимеда, включающий отношение плотности одной среды и разности плотностей двух сред:
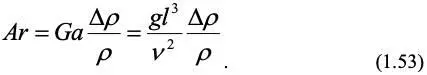
Если разность плотностей вызвана термическим расширением среды ( T– коэффициент термического расширения), то:
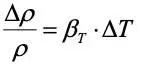
,
где Т – абсолютная температура.
После подстановки этого соотношения в критерий Архимеда получим критерий Грасгофа:

Для газов 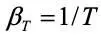 ,
,
Интервал:
Закладка:








