Сергей Семиков - Баллистическая теория Ритца и картина мироздания

F эл= μ 0I 1I 2l/2πr.

Но ведь похоже описывает взаимодействие параллельных токов и закон Ампера

F А= μ 0I 1I 2l/2πr,

дающий, правда, величину силы в полтора раза большую (Рис. 15). То есть, магнитная сила имеет электрическую природу: проводники с током притягиваются, либо отталкиваются электрической силой равной силе Ампера с точностью до коэффициента 1,5. Эта разница коэффициентов вызвана тем, что в опыте измеряют воздействие не элементов тока, а замкнутых проводников, и более точный расчёт, возможно, устранит эту небольшую разницу. К тому же, до сих пор точно не измерено отношение электрических и магнитных единиц, равное произведению скорости света на корень коэффициента в формуле Ампера [60]. Отметим, что сам Максвелл, измерив это отношение, получил, что оно не равно c = 3·10 8м/с, а, вопреки его теории, составляет в среднем 2,45·10 8м/с [152]. Это говорит в пользу коэффициента 1,5 = (3·108/2,45·108) 2.

Поскольку в опыте сложно изучать элементы тока, лучше проверять теорию, исследуя движение отдельных зарядов. Так, опыт показал, что в магнитном поле B заряд q , летящий со скоростью V перпендикулярной B , описывает окружности. Значит, на частицу действует постоянная сила Лоренца F л=qVB , направленная к центру окружности. Проверим, так ли это в модели Ритца. Для этого снова разобьём прямой проводник с током I , создающим поле B , на положительно заряженную нить и движущуюся со скоростью v отрицательную. Тогда действие F эл тока на летящий со скоростью V вдоль провода заряд сложится из двух сил (Рис. 16):

1) F 1 — воздействие неподвижной нити +τ на подвижный заряд q ;

2) F 2 — воздействие подвижной нити —τ на летящий заряд q .

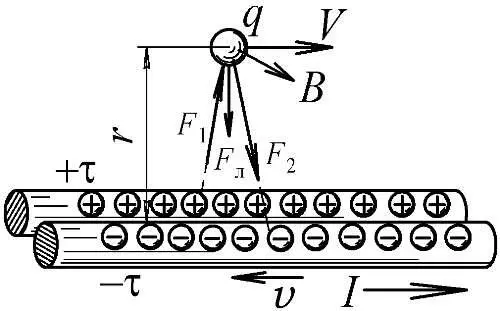
Рис. 16. Появление силы Лоренца в виде вызванной движением зарядов разности сил притяжения и отталкивания нитей.

Скорость заряда q относительно соответствующей нити равна для случая

1) V , и потому сила отталкивания

F 1= qτ/2πε 0r+qτV 2/6πε 0rc 2 ;

2) V+v , и сила притяжения

F 2= qτ/2πε 0r+qτ(V+v) 2/6πε 0rc 2 .

Отсюда сила притяжения

F эл= F 2—F 1= qτ(2Vv+v 2)/6πε 0rc 2.

Или, если учесть, что скорость летящего заряда V много больше скорости v дрейфа электронов, получим

F эл=qVvτ/3πε 0rc 2.

Итак, за счёт движения зарядов, силы F 1 и F 2 перестают уравновешивать друг друга, и проводник действует на заряд с силой, зависящей от тока I=vτ . В итоге

F эл=qVI/3πε 0rc 2 ,

или с учётом 1/c 2=ε 0μ 0 и известного выражения для поля тока B= μ 0 I /2π r найдём

F эл=qVB/1,5 .

Это с точностью до множителя 1,5 даёт силу Лоренца F л=qVB . То есть и сила Лоренца имеет чисто электрическую природу. Ту же силу легко получить из БТР и для заряда, летящего перпендикулярно проводнику. Раз сила Лоренца не зависит от направления движения заряда, то и по теории Ритца заряд должен описывать в магнитном поле B окружности, как того требует опыт.

Итак, надобность в магнитном поле отпадает, ибо то, что принято считать магнитной силой, всего лишь не скомпенсированная добавка силы электрической, созданная движением зарядов. В свою очередь, эта добавка — естественное следствие баллистической модели взаимодействия зарядов и механического сложения скорости распространения света и электрического воздействия (по сути скорости реонов) со скоростью источника. Другими словами, как это утверждали ещё Ампер и Ритц, магнитных сил и полей, вообще говоря, не существует. За их проявления мы ошибочно принимаем результат вызванного движением зарядов изменения электрических сил. Именно поэтому не удалось и никогда не удастся найти магнитные «заряды», — предсказанные Дираком монополи, существование которых казалось естественным следствием равноправия, обратимости полей и симметрии уравнений Максвелла. Выходит, что, вопреки Максвеллу, свет вполне может распространяться и без помощи магнитного поля. Наоборот, именно конечная скорость света, реонов и порождает магнитные эффекты.

Таким образом, баллистическая модель и теория Ритца не только согласуются со всеми электрическими и магнитными эффектами, но и позволяют в рамках классической картины мира понять их природу. Сама идея влияния движения заряда на величину электрической силы и объяснение через это магнитных эффектов возникла уже очень давно. Задолго до Ритца (как он сам же замечает [8]) её высказал Гаусс и развил Вебер, ещё в середине XIX века построивший на её основе электродинамику, рассматривающую магнитные и индукционные силы как следствие изменения (при движении и ускорении зарядов) сил электрических [72, 106]. Причём электродинамика Ампера и Вебера долгое время принималась учёными и противопоставлялась теории Максвелла.

Но концепция Вебера была отвергнута, причём, по иронии судьбы, — тем самым фактом, из которого должна бы была проистекать. Дело в том, что Вебер был сторонником теории дальнодействия, то есть мгновенного распространения воздействий, без помощи какого-либо промежуточного агента. А формулы свои, описывающие влияние движения на величину электрической силы, он не вывел, а эмпирически подобрал, основываясь на опытах [72, 106]. А между тем, как было показано, и как утверждал Гаусс (учитель Вебера), их можно вывести строго, придерживаясь прямо противоположного принципа, — считая, что воздействие передаётся не мгновенно, а с задержкой, через некий промежуточный агент (реоны). Предположение же о мгновенной передаче воздействия с бесконечной скоростью реонов ( c = ∞), как легко проверить, привело бы, напротив, к постоянной, не зависящей от движения зарядов величине силы. Так Ритц обосновал подход Вебера и Гаусса и тем самым завершил процесс сведения магнитных эффектов к электрическим, начатый ещё Ампером. Именно Ампер впервые понял, что магнетизм — это фикция, и магнит представляет собой лишь набор элементарных молекулярных круговых токов, то есть, в конечном счёте, — движение зарядов. Таким образом, правильнее говорить не о связи электрических и магнитных эффектов, а о том, что вторые — это лишь частное проявление первых. Интересно, что гипотезу Ампера об электрической природе магнитных сил, как следствия взаимодействия элементарных токов тел, выдвигали ещё Демокрит с Лукрецием, объяснявшие магнитное воздействие ударами микрочастиц (реонов § 4.19), источаемых магнитами и электроном (янтарём).

В том, что магнитное поле — это фикция, легко убедиться, рассмотрев два пучка электронов, летящих параллельно с одинаковой скоростью. По Максвеллу это движение зарядов создаст магнитное поле, отчего между пучками, кроме кулоновской силы отталкивания, возникнет ещё сила магнитного притяжения, как между двумя токами. Но если перейти в подвижную систему отсчёта, связанную с летящими электронами, магнитная сила исчезнет, хотя сила взаимодействия пучков по классическому принципу относительности должна остаться прежней. Свести концы с концами в теории Максвелла удаётся лишь посредством теории относительности, по которой исчезновение магнитного притяжения в точности компенсируется релятивистским снижением кулоновского отталкивания пучков [96]. Совсем как в опыте Майкельсона, где пытались объяснить отсутствие перемен при изменении скорости тем, что оно в точности компенсируется сокращением плеч интерферометра, пока не поняли, что справедлив принцип относительности (§ 1.9). Но, раз справедлив этот открытый Галилеем принцип, не проще ли считать, что и электрическая сила взаимодействия пучков не зависит от того, в какой системе она измерена, тогда как магнитная сила вообще не возникает? И действительно, электрическая сила по Ритцу, как видели, зависит не от абсолютной скорости зарядов в некой системе отсчёта, а лишь от их взаимной скорости по отношению друг к другу. Именно эта зависимость, доказывающая, что заряд сообщает свою скорость воздействиям, и воспринимается нами в форме магнитных эффектов.