Сергей Семиков - Баллистическая теория Ритца и картина мироздания

До сих пор, рассуждая о баллистическом принципе сложения скорости света со скоростью источника, мы говорили о движении света в вакууме. Если же электромагнитная волна летит в среде, то, как было отмечено выше, ситуация кардинально меняется: проходя через среду, будь то воздух или плотные тела, волна воздействует на электроны среды, приводя их в колебания, отчего те излучают вторичные волны, которые, слагаясь с исходной, рождают явления рефракции, дисперсии и дифракции. Поэтому, возникает уже избранная система отсчёта, связанная с материальной средой. Описание волн в такой среде во многом подобно описанию их с помощью эфира. Вот почему теория Максвелла, основанная на эфире, всё ещё используется, не обнаруживая расхождений с опытом. Однако, в космосе, в безвоздушном пространстве, — возникают отклонения от теории Максвелла. Судя по результатам радиолокации и астрономических наблюдений, исчезает преимущественная система отсчёта, связанная с атмосферой, и скорость света начинает зависеть от скорости источника (Часть 2).

В данном разделе нас будут интересовать именно опыты в земных лабораториях, где свет движется в среде. Так, в качестве противоречащего БТР иногда приводят известный опыт по влиянию движения источника на скорость света в среде, — опыт Физо [93, 153]. По его результатам, если источник движется навстречу среде со скоростью V , то в среде фазовая скорость света от этого источника уже не c/n , а c/n+V/n 2 . Паули считал это доказательством того, что скорость источника не складывается по классическому закону со скоростью света. Но, как было сказано, баллистический принцип здесь и не обязан работать, ибо скорость света в среде определяется не одним только источником, а ещё и атомами среды, вторичное излучение которых складывается с начальным, образуя новую волну. Вычислим её фазовую скорость [136, с. 425]. Если свет имеет скорость c+V , то поле единичной падающей волны опишется уравнением

E 0=e i(ωt — k'x),

где ω — циклическая частота падающей волны, а k'= ω/( c+V ) — её волновое число.

Эта волна возбуждает в среде вторичные волны интенсивности

E 1= — ikxbe i(ωt — kx) [136],

где k= ω/ c — их волновое число, x — толщина пройденного слоя вещества, излучающего новую волну (Рис. 38), b — безразмерный коэффициент, характеризующий оптическую плотность среды (концентрацию атомов и эффективность переизлучения ими волны с частотой ω). Поле результирующей волны

E= E 0+E 1= e i(ωt — kx)(e ix(k — k')—ikxb),

что с учётом разложения e x ≈1+ x при малых x и ( k — k' )≈ ω V / c 2= kV / c даёт

E≈e i(ωt — kx)(1+ ikxV/c— ikxb)≈ e i(ωt — kx(1+b — V/c)).

Здесь kx ( b — V / c ) — это сдвиг фазы, растущий вместе с пройденным светом путём x и тем самым меняющий фазовую скорость света c* . По сути, в среде волновое число k= ω/ c заменяется новым k*= ω/ c*= k (1+ b — V / c ). Отсюда c*= ck/k* = c/ (1 +b — V / c ). Если V= 0, то получим обычную скорость света в среде c*= c/ (1+ b ), где (1+ b ) — коэффициент преломления n . Если же скорость V отлична от нуля, получим: c*= c/ (1 +b — V / c )= c/ ( n — V / c )≈ c/n+V / n 2. Таким образом, в среде движение источника меняет фазовую скорость света не на V , а только на V / n 2. Относительно источника скорость света в среде c'= c*—V = c/n — V (1–1/ n 2). Коэффициент 1–1/ n 2называют френелевским коэффициентом увлечения. Итак, если на базе молекулярной оптики учесть переизлучение света средой, то БТР легко объяснит опыт Физо и даёт верное выражение для коэффициента увлечения Френеля.

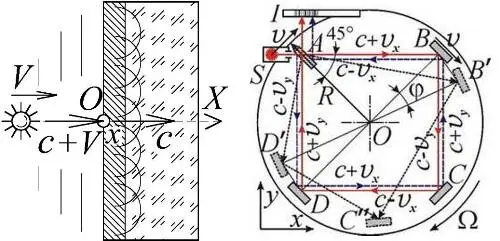
Рис. 38. Отказ принципа относительности в опытах Физо (слева) и Саньяка (справа).

Как видим, наличие среды нарушает равноправие систем отсчёта. Во-первых, свет в среде движется со скоростью, отличной от скорости света в этой среде c/n . А, во-вторых, не вся скорость источника передаётся свету. Но реально здесь нет никакого противоречия с галилеевым принципом относительности. Рассмотрим для пояснения известную иллюстрацию принципа относительности, предложенную самим Галилеем. В своём "Диалоге" он показал, что мы не сможем заметить равномерного движения корабля, находясь в его трюме. Предметы в трюме будут падать совершенно так же (отвесно вниз), как в неподвижном корабле. Происходит это оттого, что скорость v корабля сообщается падающим предметам. Но если и сам корабль и падающие в нём предметы движутся по горизонтали со скоростью v , то их относительное движение нельзя заметить. Но так будет только в трюме. Если мы выйдем на палубу корабля, то равноправие уже нарушается. За счёт движения корабля обдувающий его воздух порождает встречный ветер, который нарушает симметрию, увлекает предметы. Поэтому брошенные от носа к корме предметы, увлекаемые ветром, будут долетать быстрее и дальше, чем от кормы к носу. Подобно воздуху, увлекающему в опыте Галилея падающие предметы, среда передаёт частично скорость и свету. В опыте Майкельсона среда не нарушала принцип относительности и баллистический принцип лишь потому, что атмосфера двигалась вместе с Землёй и источником света, так же как воздух в трюме корабля двигался вместе с кораблём в опыте Галилея. Зато при взаимном движении источника и среды ситуация кардинально меняется: принцип относительности перестаёт соблюдаться.

Итак, если движущийся источник сообщает свою скорость свету, в качестве добавки к скорости c , то, при попадании в прозрачную среду, за счёт вторичного излучения среды и сложения его с излучением падающей волны, эта добавка постепенно исчезнет, как постепенно теряет горизонтальную скорость предмет, выброшенный из окна поезда и тормозимый сопротивлением воздуха. Исходная волна, попадая в среду и заставляя колебаться её электроны, переизлучается этими бесчисленными ретрансляторами и, при том, гасится за счёт интерференции с идущими от них вторичными волнами. Этот принцип известен в электродинамике как "теорема погашения Эвальда и Озеена". Однако в применении к БТР эта теорема была впервые исследована Дж. Фоксом [2], который показал, что, вместе с гашением первичной волны, теряется также информация о скорости её источника. Поэтому, в дальнейшем будем иногда называть это правило погашения у света добавочной скорости источника — "принципом Фокса". Этот принцип имеет большое значение в изучении многих явлений космоса и особенно важен в земных лабораторных экспериментах.

Интересно отметить, что некоторые лабораторные эксперименты действительно подтвердили, что свет после прохождения сквозь среду приобретает её скорость. Ведь, согласно БТР, скорость равна c относительно источника. Среда же, через которую проходит свет, сама начинает играть роль источника света. И точно, как показали уже земные эксперименты, скажем опыты У. Кантора [4] и М.И. Дуплищева [47], прозрачные пластинки дополнительно сообщают свою скорость v излучению, отчего скорость световых лучей становится не c , а c+v . Результаты этих экспериментов, несмотря на их тщательную постановку, пытались оспорить и затушевать [153]. Однако достаточно убедительно этого никто не сделал.