Сергей Семиков - Баллистическая теория Ритца и картина мироздания

По той же причине не могут ни подтвердить, ни опровергнуть баллистической теории другие опыты по измерению скорости света от движущихся космических источников, выполненные в земной атмосфере. Так, по предложению Ла Розы [93] пробовали использовать для проверки БТР схему опыта Майкельсона, применив в качестве источников света движущиеся или вращающиеся с большой скоростью Солнце (опыт Д. Миля), планеты, звёзды (опыт Р. Томашека) [6, 152]. Поскольку в опыте мерялись величины второго порядка малости по v/c , то даже учёт изменения скорости света, при отражении от зеркала, не помешал бы обнаружить различие в скорости лучей. Тогда опыт действительно получался бы в точности аналогичен опыту Майкельсона, только роль неподвижной среды, относительно которой свет имел бы постоянную скорость, играл бы не эфир, а система отсчёта, связанная с источником. Однако, все эти опыты тоже не выявили какой-либо зависимости интерференционной картины от скорости источника света и положения установки. Впрочем, причина этого, опять же, состояла не в утверждавшейся авторами опытов ошибочности БТР, а в том, что свет, изучаемый в опыте, испускался уже не движущимися источниками, а покоящимися переизлучающими атомами атмосферы, зеркалами оптической системы и линзами телескопов. Прежде, чем скорость света была измерена, он успевал сотни раз переизлучиться и преобразоваться на пути следования луча. Исследовался не свет космических источников, а свет неподвижных земных. Уже одна атмосферная рефракция (искривление атмосферой звёздных световых лучей) говорит о том, что мы наблюдаем не исходный свет космического источника, а вторичное излучение атмосферы, идущее в совсем ином направлении.

Впрочем, не всегда для проверки БТР применялись измерения света в земной атмосфере. Порой, путь, на котором у лучей, испущенных разными космическими источниками, набиралась разность хода, пролегал и в космосе. Так, для проверки баллистического принципа Е.Б. Александров предлагал использовать цефеиды [14]. Если эти звёзды пульсируют (периодически раздуваются и сжимаются), то от разницы лучевых скоростей в разных участках поверхности неравные скорости обретут и световые лучи, которые будут от этого восприниматься не одновременно. Это привело бы к "размыву" вспышек цефеид, сделав их незаметными для нас. Но, согласно БТР, колебания блеска цефеид вызваны не пульсацией, а эффектом Ритца от обращения звёзд в двойных системах (§ 2.12), потому и нет разброса скоростей от их пульсации. По иронии судьбы, сразу вслед за статьёй Е. Александрова, критикующего БТР, в "Астрономическом журнале" стоит статья Э.Ф. Бражниковой и С.В. Бабинчука, где описан, по сути, эффект Барра (§ 2.10), как раз подтверждающий справедливость БТР в космосе для двойных звёзд.

Согласно Е.Б. Александрову, колебания блеска цефеид могли бы размываться и за счёт теплового разброса скоростей элементарных атомных излучателей, придающих разные скорости испущенному ими свету [14]. На деле же, рассеивающая свет среда должна излучать как одно целое. Важна скорость всей среды, а не отдельных её излучателей. Рассеяние атомами, переизлучающими свет по принципу Фокса, сглаживает начальный разброс скоростей света, на что обратил внимание и сам Фокс, отвечая на аргументы Александрова [2]. Так, если излучение одного атома рассеивается на двух других, то свет, переизлучённый приближающимся атомом, увеличит скорость на V , а удаляющимся — уменьшит.

От разной скорости волны приходят к новым атомам уже в противофазе и гасят друг друга (Рис. 64). Это произойдёт на таком расстоянии S , на котором разность хода S ( c+V )/ c — S ( c — V )/ c достигнет половины длины волны λ. То есть 2 SV / c = λ/2, откуда S = λ c/ 4 V . При средней скорости атомов в звёздных атмосферах V ~1000 м/с и длине волны λ~1 мкм это даст S =75 см. Значит, уже объёмы газа с размерами более 1 м должны излучать как одно целое. Волны, излучённые с разной скоростью, будут постепенно гаситься интерференцией, зато волны, излучаемые сходно движущимися атомами, — будут взаимно усиливаться. В итоге, свету передаётся только та скорость атомов, с которой они движутся вместе со средой, и тепловой разброс скорости света отсутствует. Он возможен лишь у разреженных сред и малых объёмов газа.

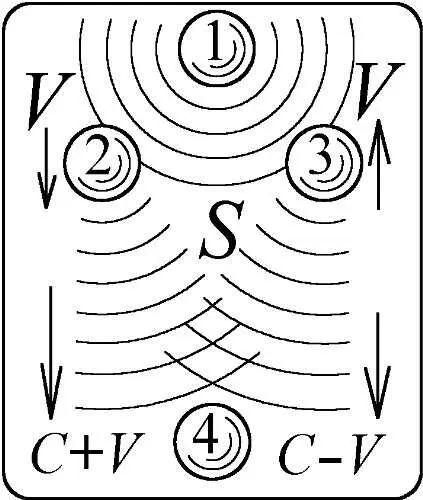
Рис. 64. В участке среды усиливается излучение атомов, для которых V=0.

Некоторые астрономы, скажем О. Хэкман, Р. Диккенс и С. Малин, пытались опровергнуть БТР, используя звёздную аберрацию (§ 1.9). Известно, что орбитальное движение Земли с V= 30 км/с меняет направление прихода звёздного света на угол α= V/c . Это — прямое следствие классического закона сложения векторов скорости света и источника. Но, если бы скорость света зависела от лучевой скорости v источника, то у разных объектов отклонение α было бы разным: вместо α= V/c нашли бы α= V /( c — v ). Интересно, что такое неравенство аберрационных углов предсказывали и тщетно искали ещё Лаплас и Араго, которые поддерживали корпускулярную теорию света и применяли к нему баллистический принцип (см. "Эйнштейновский сборник-1977"). Впрочем, при имеющихся скоростях звёзд, различие углов α вышло бы столь малым, что его и не смогли бы заметить. Ведь даже для быстрейших звёзд, летящих со скоростью v ~300 км/с, то есть 0,001 c , изменение α составило бы одну тысячную. А поскольку угол аберрации α и сам крайне мал — всего 20 угловых секунд, — то его изменение на 0,02'' будет и вовсе незаметно, даже при наблюдении через лучшие телескопы с разрешением в 1''–0,1''.

Впрочем, полагали, что изменение α можно выявить у далёких галактик, которые, как судят по эффекту Доплера, удаляются с огромными скоростями v , сопоставимыми со скоростью света c . И, всё же, для них угол α= V /( c — v ) оказался тем же, что и для звёзд, словно скорость v не меняла скорости света, тем самым говоря будто бы против БТР [153]. Здесь нестыковка возникала опять же от неверных представлений о космосе. Ведь, согласно БТР, галактики не разбегаются, а имеют сравнительно небольшие случайные скорости, такие, что v/c <<1, тогда как красное смещение вызвано не эффектом Доплера от удаления галактик, а эффектом Ритца от их вращения (§ 2.4). Поэтому реальная скорость v галактик ничтожна в сравнении со световой и очень слабо влияет на скорость идущего от галактик света. Именно поэтому, аберрационный угол мало отличается от стандартного α= V/c . Кстати, это отмечал и сам автор "опровержения", Диккенс, понимавший, что оно теряет смысл (аберрация света галактик не противоречит БТР), если красное смещение галактик имеет недоплеровскую природу, согласно Белопольскому и другим астрономам [87].