Сергей Семиков - Баллистическая теория Ритца и картина мироздания

Итак, явления космоса не противоречат, а скорее подтверждают теорию Ритца. В большинстве же своём постановка и трактовка таких опытов попросту не корректна и не позволяет установить ни справедливость, ни ошибочность БТР. Так что нужны новые наблюдения и эксперименты, скажем, сравнение аберрационных углов звёзд интерферометрическими методами с их разрешением в 0,001''-0,0001'', которые докажут БТР окончательно. И тогда уже, совсем как в романе Жюля Верна, отпадут всякие сомнения в могуществе баллистики.

Как видим, приведённые выше попытки опровергнуть баллистический принцип не имеют доказательной силы, — все они некорректны. Впрочем, не они привели к отказу от баллистической теории Ритца, а совсем иные наблюдения, а, конкретней, выполненный Де Ситтером анализ движения двойных звёзд. Собственно говоря, это и был первый весомый аргумент против баллистической теории, который остановил её развитие и привёл к забвению идей Ритца. Напомним, что "двойной звездой" называют пару звёзд M и N , обращающихся вокруг общего центра O по круговым или эллиптическим орбитам (Рис. 65). Если скорость испускаемого звёздами света c складывается с их орбитальной скоростью v , то луч от приближающейся к нам звезды A должен иметь бóльшую скорость и проходить расстояние L до земного наблюдателя быстрее, чем луч от удаляющейся B (Рис. 63. а ). Поэтому, согласно БТР, свет приближающейся звезды M мы видели бы на время Δ t = L /( c-v )— L /( c+v ) раньше, чем свет удаляющейся N . То есть, в одних точках орбиты мы будем наблюдать звезды чуть раньше, а, в других, — чуть позже, чем следовало бы.

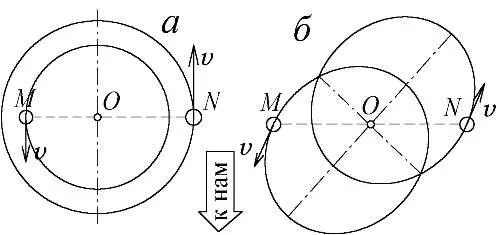
Рис. 65. Двойные звёзды с круговыми (а) и эллиптическими (б) орбитами.

В результате видимое движение звёзд исказится, получив отклонения от законов Кеплера, чего реально никто не наблюдал [26, 152]. Именно это было основным аргументом, по которому в своё время отвергли теорию Ритца. Но, поздней, было показано, что у двойных звёзд, различимых через телескоп, подобные отклонения и нельзя бы было обнаружить при существующих параметрах двойных звёздных систем и разрешающей способности астрономических приборов [111]. Из-за сравнительно малой их удалённости, малыми (меньше разрешающей силы телескопов) получаются и пропорциональные L искажения.

Поэтому, против теории Ритца могут свидетельствовать лишь наблюдения спектрально-двойных звёзд, удалённых от нас на много большие расстояния, чем визуально-двойные, и имеющих пропорционально большие искажения. Однако, такие звёзды уже неразличимы по отдельности, и, даже при наблюдении через сильнейшие телескопы, сливаются в одну светящуюся точку. Поэтому, об их движении судят лишь на основании наблюдений спектра звёзд: смещение спектральных линий даёт по формуле эффекта Доплера лучевую скорость звёзд в каждый момент времени. А по кривой лучевых скоростей легко найти основные параметры звёздных орбит, в том числе их эксцентриситет, — степень вытянутости орбиты. Так, если для круговой орбиты кривая лучевых скоростей имеет форму синусоиды (Рис. 66. а ), то для эллиптической орбиты она уже менее симметрична (Рис. 66. б, в ).

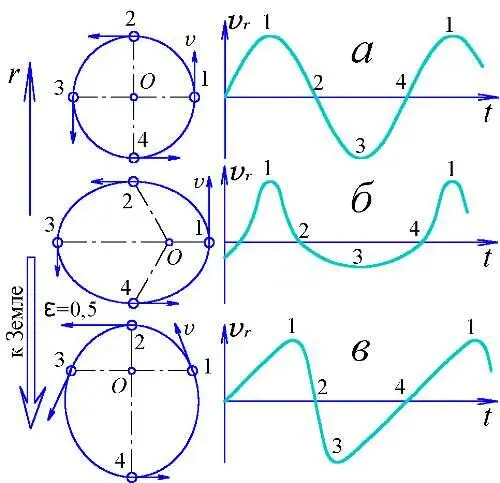
Рис. 66. Орбитальные v и лучевые vr скорости звёзд в зависимости от вида их орбиты и положения на ней.

Рассмотрим случай круговой орбиты. Если движение звезды влияет на скорость света, то её кривая скоростей должна перекоситься (Рис. 67): точки, где лучевые скорости v r положительны (направлены от нас, снижая скорость света до c - v r ) сместятся вперёд по оси времени (их свет запоздает), а где отрицательны — назад (их свет прибудет раньше за счёт выросшей скорости света). И форма кривой скоростей (Рис. 67. а ) стала бы напоминать таковую для эллиптической орбиты Рис. 66. в ). Кроме того, нарушался бы (Рис. 67. б ) зеркальный ход кривых скоростей двух звёзд M и N (Рис. 65. а ). Зная удалённость и скорость звёзд, легко вычислить значения этих предполагаемых отклонений. Но, как показали наблюдения, такие отклонения отсутствуют или имеют величину заметно меньшую расчётной. Так, известно множество спектрально-двойных с почти круговыми орбитами, которые по БТР казались бы сильно вытянутыми. Выяснилось, что, если скорость света и складывается со скоростью источника по закону c΄=c+kv , то k <0,002 [93]. То есть выходило, что теория Ритца (где k =1) полностью противоречит наблюдениям.

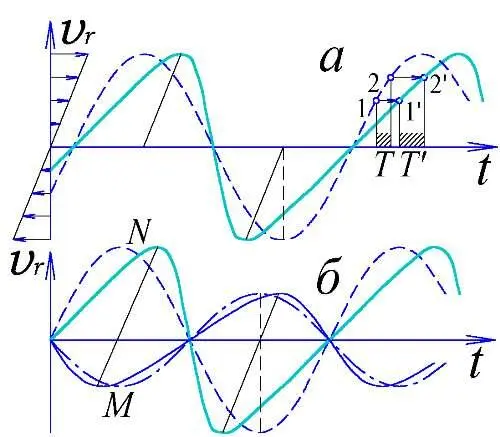
Рис. 67. Искажения (сплошные линии) кривых скоростей, вносимые движением звёзд.

Но всё не столь однозначно. Ведь о движении спектрально-двойных судят лишь по смещению спектральных линий, а в БТР оно создаётся уже не только доплер-, но и ритц-эффектом (§ 1.10). Причём, в космосе, в мире гигантских масштабов L , ритцевы смещения, пропорциональные La / c 2, могут заметно превосходить доплеровские, пропорциональные ν / c . Для звезды, движущейся по круговой орбите радиуса r , центростремительное ускорение a = v 2/ r , откуда La / c 2= Lv 2/ rc 2. И спектральный сдвиг от эффекта Ритца превосходит таковой от эффекта Доплера в Lv / rc , или порядка L / cP раз, то есть, — во столько же раз, во сколько расстояние до звезды в световых годах L / c превышает период P =2π r / v её обращения. А, поскольку, для большинства спектрально-двойных звёзд, исследованных Де Ситтером, орбитальный период P составлял несколько суток, а удалённость L / c — многие световые годы, то смещение для них создавалось в основном эффектом Ритца.

Следовательно, в спектрах тесных двойных звёздных систем периодическое смещение линий вызвано, по большей части, не скоростями, а ускорениями звёзд. Найденные же по формуле Доплера параметры движения — ошибочны: истинные скорости звёзд будут меньше найденных — как раз в L / cP раз, то есть, как минимум, в тысячи раз. А, потому, ожидаемые отклонения, пропорциональные kv , не могли бы возникнуть даже при k =1: наблюдения не противоречат теории Ритца! Напротив, раз реальные отклонения, согласно теории Ритца, в тысячи раз меньше ожидаемых Де Ситтером, то обнаруженные искажения (соответствующие k <0,002) могут служить подтверждением БТР. Если б астрономы смогли наблюдать движение спектрально-двойных звёзд непосредственно, они бы заметили несоответствия, но в том-то и проблема, что о движении их судят лишь по спектрам, а переменное лучевое ускорение звёзд создаёт кривые спектрального смещения, схожие с кривыми лучевых скоростей (сравните Рис. 66 и Рис. 68).