Сергей Семиков - Баллистическая теория Ритца и картина мироздания

Собственно говоря, именно эта модель и позволила впервые найти весь спектр частот, излучаемых атомом водорода, причём столь оригинальным путём, что он и сегодня заслуживает внимания, как показано в замечательной статье [50]. Ритц не применял квантовых идей: электромагнитные волны в его модели генерировали не абстрактные квантовые переходы, а классические колебания электронов. Ещё до Резерфорда Ритц понял, что движением электрона в атоме управляет некий центральный механизм, остов, скелет атома, называемый ядром. Но Ритц, в отличие от Резерфорда, догадался, что управление это осуществляют не электрические, а магнитные силы, за что его модель атома и была названа "магнитной".

Мы привыкли считать, что электроны в атоме движутся по орбитам — под действием электрического притяжения ядра, забывая, что сами на практике, — в ускорителях частиц, плазменных установках и индукционных печах — задаём круговые движения электронов с помощью магнитных полей. В своей работе 1908 г. "Атомные магнитные поля и спектральные серии" Ритц убедительно показал, что только силами магнитной природы можно объяснить спектры излучения атомов. Согласно ему, магнитное поле атома создано набором последовательно соединённых элементарных магнитиков стандартного размера a , образующих вытянутый магнитный стержень (Рис. 94). Вместо магнитов можно взять витки с током, составляющие катушку индуктивности, соленоид с постоянным шагом витка a . Как показал Ритц, в зависимости от числа магнитов (витков) стержень создаёт такие магнитные поля, в которых электрон должен колебаться с теми частотами, что были найдены в спектре атома водорода.

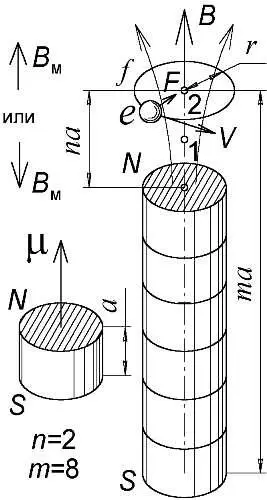
Рис. 94. Магнитная ось, набранная из магнитов, управляет полётом электронов.

При всей кажущейся наивности представления атома в виде некоего прибора (гибрида циклотрона и магнитной антенны), модель Ритца не только верно описала водородный спектр и эффект Зеемана, но и предсказала новые спектральные серии водорода и других элементов, поздней действительно открытые. Но трагическая ранняя гибель Ритца в 1909 г., спустя год после публикации его баллистической теории и модели атома, позволила о них забыть, хотя открытыми с их помощью принципами учёные не побрезговали и пользуются ими до сих пор. В свете открытий ушедшего столетия, которое не внесло ясности в квантовую модель атома, а лишь запутало её, модель атома Ритца обретает новое звучание и смысл.

Так, открыли, что у каждого электрона есть стандартный магнитный момент μ, наделяющий электрон свойствами элементарного магнитика. Тем же магнитным моментом μ обладает и открытый в 1932 г. антиэлектрон, — позитрон. Представим теперь, что позитрон соединился с электроном, и этот диполь стал одним концом притягивать электроны, а другим — позитроны. В итоге, электроны и позитроны, последовательно цепляясь друг за друга паровозиком, могут сливаться в протяжённые прямые цепи, в которых все магнитики (магнитные моменты) электронов и позитронов ориентированны одинаково. Расстояния между их центрами окажутся постоянными, одинаковыми: порядка размера электрона a (Рис. 95). Как было показано (§ 1.16), при контакте электронов с позитронами они вовсе не уничтожаются, а просто слипаются в нейтральную частицу, оказываясь разделены расстоянием, равным классическому радиусу электрона.

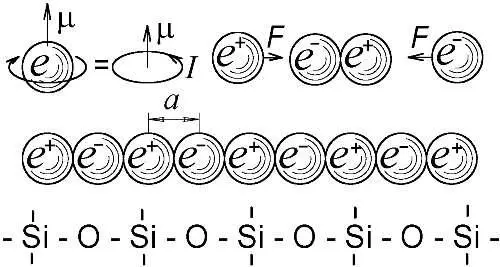
Рис. 95. Магнитный момент электрона как результат вращения. Слияние электронов с позитронами в цепочки типа линейных молекул силикона и игольчатых кристаллов.

Итак, магнитные стержни, оси, набранные из элементарных магнитиков, которые Ритц только предполагал, в принципе могут вырастать сами, подобно кристаллам соли из чередующихся ионов Na+ и Cl-, или линейным молекулам полимеров, построенным из тысяч одинаковых звеньев, к примеру, — из чередующихся атомов Si и O (силикон). Стержни, содержащие равное число электронов и позитронов, не имели бы заряда, но породили бы заметное магнитное поле. Поэтому, оказавшийся возле стержня электрон не был бы ни отторгнут, ни притянут, но мог бы совершать в магнитном поле стержня круговые движения возле точки равновесия с частотой f , не зависящей от его скорости V и радиуса орбиты r (Рис. 94). В магнитном поле с индукцией B на электрон с зарядом e и массой M действует сила Лоренца F = eVB , заставляющая его двигаться по окружности с центростремительным ускорением ar = V 2/ r . Поскольку Ma r = F , имеем MV 2/ r = eVB , откуда угловая скорость электрона 2π f=V / r = Be / M . То есть, частота f = Be /2π M обращения электрона, равная частоте излучаемого им света, зависит лишь от индукции поля B , поскольку величина e /2π M постоянна.

Однако, спектры излучения атомов состоят из дискретного ряда частот. Значит, и поле B может принимать лишь определённые значения. Это заставило Ритца предположить, что электрон способен занимать в атоме лишь некоторые устойчивые положения, каждому из которых присуще своё значение поля B , задаваемое расстоянием электрона до стержня. Эту мысль о наличии в атоме устойчивых положений и орбит электрона, Ритц, в отличие от Бора, развивал в рамках классического, а не квантового подхода. Он считал, что раз стандартны расстояния и размеры a магнитов, то тем же расстоянием a должны быть отделены и возможные, разрешённые положения электрона — узлы 1, 2, 3…, где он способен пребывать (Рис. 94).

Именно так и вёл бы себя электрон возле электрон-позитронного стержня, который за счёт неравномерного (дискретного) распределения зарядов создаёт небольшое продольное электрическое поле. Поэтому, где бы ни находился электрон, он всегда стремится встать против положительного позитрона, а возникающая при смещении электрона продольная сила возвращает его на место (Рис. 96). То есть, электрон способен устойчиво занимать положения — лишь напротив позитронов, и может "прыгать" вдоль стержня только на расстояние 2 a .

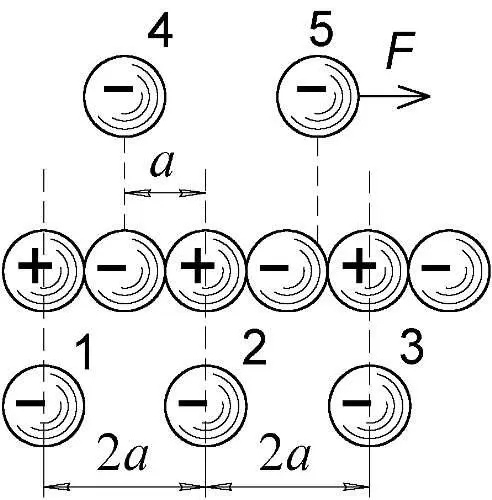
Рис. 96. Устойчивые (1, 2, 3) и неустойчивые (4, 5) положения электрона возле цепочки.

Но смещение электрона вдоль стержня не влияет на величину магнитного поля. Да и Ритц считал, что у электрона кратно а меняется расстояние до магнита. Поэтому, приходим к выводу, что в атоме не один, а два стержня, две магнитных оси, соединённых перпендикулярно, наподобие перекладин креста (Рис. 97). Электрон, размещаясь против позитронов каждой оси, должен находиться в одном из узлов сетки, образованной линиями уровня позитронов, и его расстояние до каждого стержня будет кратно 2 a . Потому, и поле B меняется прерывисто. Итак, в крестовой магнитной модели атома электрон и впрямь может занимать лишь некоторые устойчивые положения, возле которых и колеблется в магнитном поле крестовины. И, что очень важно, эта дискретность вводится в рамках классической физики. Подробнее о причинах устойчивости таких положений электронов расскажем далее (§ 3.2, § 4.14).