Вилли Лей - Ракеты и полеты в космос

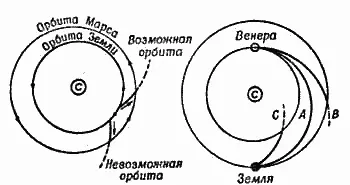
Рис. 74. Орбиты Гоманна. Слева - возможная орбита, двигаясь по которой тела следуют общему вращению солнечной системы, и невозможная орбита. Справа - три возможных орбиты, из которых одна (А) требует наибольшего времени и самого минимального расхода топлива.

Рассчитывая «возможные» орбиты-траектории, доктор Гоманн намеренно упростил расчеты, приняв, что орбиты внутренних планет лежат точно в одной плоскости и что они круглые, а не эллиптические. Последнее допущение имеет целью избавиться от усложняющего все расчеты факта, что планеты движутся в перигелии несколько быстрее, чем в афелии. Гоманн допустил также, что средняя орбитальная скорость планеты является верной для каждой точки орбиты. Выражаясь более научно, он допустил, что радиус-вектор в равные промежутки времени проходит равные участки и описывает равные углы.

Первым примером Гоманна был полет на Венеру. Взяв пять «возможных» орбит, он обозначил их А, В, С, D и Е. Орбита А касается орбиты Венеры и орбиты Земли; орбита В пересекает орбиту Земли, но касается орбиты Венеры; орбита С касается орбиты Земли, но пересекает орбиту Венеры. Орбита D сходна с орбитой С, но более полога, а орбита Е ничем не отличается от орбиты В. Предполагалось, что космический корабль, достигая Венеры, уравнивает свою скорость с орбитальной скоростью планеты, но не производит посадки. Конечный вес корабля к этому времени принимается равным 6 т, включая трех пассажиров.

Характеристики полетов по этим орбитам приведены в следующей таблице:

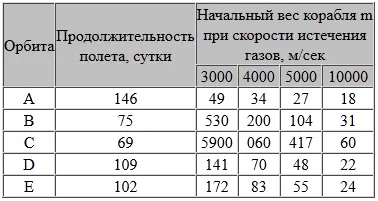
Эта таблица позволяет сделать один-единственный вывод: для практических целей могут быть взяты только орбиты типа А. Любая орбита, пересекающая орбиту планеты и вызывающая необходимость изменения направления, не может рассматриваться как «возможная». Указанные выше цифры требуют одной оговорки. Они не означают, что, например, шеститонный корабль, имея скорость истечения газов порядка 5000 м/сек, потребует 21 т топлива, чтобы достичь Венеры за 146 дней, или 43 т топлива при скорости истечения 3000 м/сек. Если бы все дело сводилось только к этому, мы уже сейчас могли бы заняться непосредственно созданием космического корабля. Эти цифры выражают лишь ту «дань», которую космический корабль должен «уплатить» Солнцу для выхода с орбиты Земли на орбиту Венеры и для уравнивания своей скорости со скоростями обеих планет.

В расчетах Гоманна не учтено, что обе планеты обладают определенной силой притяжения. Поэтому в таблице нет данных о времени и топливе, необходимых для выхода корабля из сферы притяжения Земли и возвращения на Землю.

Таким образом, 146 дней—это продолжительность полета только в одном направлении. Рассчитанная по этому способу продолжительность полета на Марс по орбите типа А составила бы 258 дней.

Теперь попытаемся определить продолжительность полета космического корабля по одной из «возможных» орбит туда и обратно. Это не означает, что, например, при полете на Венеру или на Марс придется просто удвоить полученные Гоманном результаты. Допустим, что корабль, двигаясь по орбите А, достиг Марса, но не совершил посадки, а сразу же лег на обратный курс. Может показаться, что в этом случае нет нужды уравнивать скорость корабля со скоростью Марса, а следует просто остаться на той же орбите. Через определенное время, даже не расходуя топлива, корабль так или иначе непременно вернется на орбиту Земли. Но это неверно, так как к моменту выхода корабля на орбиту Земли наша планета окажется уже в другой точке орбиты.

Когда мы стартуем с Земли, более «медленный» Марс должен быть далеко впереди. Время старта рассчитывается так, чтобы корабль догнал планету. Но за 258 дней относительна «быстрая» Земля уйдет вперед, и потому к концу полета корабля Земля будет находиться далеко от той точки, в которой произойдет смыкание орбит возвращающегося корабля и Земли, В силу этого корабль должен будет выждать либо на Марсе, либо вблизи него, пока Земля не окажется позади Марса. Этот период ожидания довольно продолжителен и составляет 455 дней. Таким образом, полет на Марс и обратно требует 258 + 455 + 258 = 971 день, то есть около двух земных лет и восьми месяцев (рис. 75).

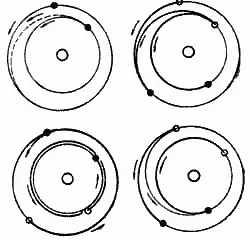
Рис. 75. Полет на Марс и обратно:

Вверху слева - положение Земли и Марса (черные кружки) в начале полета космического корабля, траектория которого показана пунктиром;

справа - положение в момент прибытия корабля на Марс (предыдущее положение планет отмечено белыми кружками);

внизу слева - положение в момент вылета с Марса, Марс завершил часть оборота, лежащую между белым и черным кружками, а Земля сделала вокруг Солнца почти 1,25 оборота;

справа - положение в момент возвращения космического корабля на Землю.

Полет на Венеру осуществляется в условиях, прямо противоположных условиям полета на Марс, так как Венера движется по орбите быстрее Земли, однако и здесь обязательным будет период ожидания на Венере или вблизи нее продолжительностью немного более 470 дней. Следовательно, весь полет на Венеру и обратно займет примерно 146 + 470 + 146 = 762 дня, то есть два земных года и один месяц.

Теперь рассмотрим проблему соотношения масс корабля при межпланетных полетах. В приведенной ниже таблице даны отношения масс для ракет, стартующих с Земли.

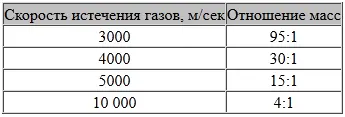
Эта таблица составлена с учетом сопротивления воздуха и умеренного ускорения, которое может выдержать пилот корабля. Если нужно определить, какая первоначальная масса необходима для полета на Венеру, следует выбрать скорость истечения, взять соответствующую цифру для полета на Венеру из таблицы на стр. 327 и умножить ее на цифру для той же скорости истечения из данной таблицы. Это, конечно, весьма примитивный способ производства расчетов с точки зрения математики, но с его помощью можно быстро получить ориентировочные данные.

Полет, описанный Гоманном, протекает следующим образом: ракетный корабль стартует вертикально с Земли в произвольном направлении и удаляется от нее на 80 000 км. На этом расстоянии влияние гравитационного поля Земли столь ничтожно, что им можно пренебречь. Корабль здесь становится независимым от Земли, но все еще сохраняет ее орбитальную скорость. Стоит увеличить орбитальную скорость корабля хотя бы на 3, 2 км/сек— и он будет двигаться внутрь солнечной системы по орбите типа А. Во время подъема и выхода из сферы притяжения Земли, продолжающихся несколько дней, ракетные двигатели должны работать в общей сложности около 8 минут; для изменения орбитальной скорости корабля они включаются еще на 2 минуты. После того они не работают до тех пор, пока корабль не выйдет на орбиту Венеры. Двигаясь внутрь солнечной системы, то есть фактически «падая» по направлению к Солнцу, корабль набирает скорость; поэтому он будет двигаться даже несколько быстрее Венеры. Эта разница в скоростях должна быть урегулирована, после чего оба тела будут двигаться по одной орбите и с одинаковой скоростью. Но это будет продолжаться недолго. Гравитационное поле планеты увлечет корабль «вниз», и начнется посадочный маневр, целью которого будет погасить скорость, увеличившуюся под действием силы притяжения планеты.