Вадим Грибунин - Цифровая стеганография

Перечисленные причины приводят к модели стегосистемы, в которой нарушитель может быть способен определить, что статистика наблюдаемых им в канале последовательностей отличается от известной ему статистики контейнеров, но он не способен установить причину этих отличий. Таким образом, нарушитель хотя и подозревает о существовании скрытого канала, но не может доказать или опровергнуть этого. Требуемые доказательства могут быть получены, если нарушитель сумеет прочитать скрываемое сообщение. Методами теории информации опишем стойкость стегосистемы к чтению скрываемых сообщений.

В работе [2] несколько с иных позиций, чем в подходе Качина [3] определяется стойкость стегосистемы. Стегосистема называется теоретико-информационно стойкой, если нарушитель не способен получить никакой информации о встроенном сообщении, анализируя перехваченные стего при условии знания статистических характеристик пустых контейнеров. В рамках этого определения подсчитывается взаимная информация 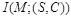между скрываемыми сообщениями М и множествами стего S и соответствующих им контейнеров C . В теоретико-информационно стойкой, или, иначе говоря, совершенной стегосистеме должно выполняться равенство 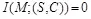. Как известно из теории информации [10], взаимная информация может быть определена через безусловную и условную энтропию:

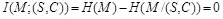. (4.8)

Это дает фундаментальное условие стойкости стегосистемы вида

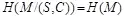. (4.9)

Такое определение теоретико-информационной стойкости стегосистемы очень напоминает соответствующее определение теоретико-информационной стойкости системы шифрования информации. Если неопределенность нарушителя относительно сообщения М не уменьшается при перехвате криптограммы Е , то по определению К.Шеннона данная система шифрования является совершенной [7]:

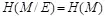. (4.10)

Заметим, что выражения (4.9) и (4.10) указывают, что нарушитель не способен определить ни одного бита защищаемого сообщения. При этом для системы шифрования точно известно, что в криптограмме это сообщение содержится. Для стегосистемы выражение (4.9) может выполняться в следующих случаях:

1. Стегосистема не используется.

2. Осуществляется скрытая передача информации, используется совершенная к установлению факта наличия скрытой связи стегосистема. Если нарушитель не способен определить факт наличия скрываемого сообщения, то тем более он не способен прочитать ни одного бита этого сообщения.

3. Осуществляется скрытая передача информации, нарушитель способен определить факт наличия скрытой связи. Однако он не способен прочитать ни одного бита скрываемого сообщения.

Например, третий случай был описан в предыдущем параграфе при вложении безизбыточных скрываемых сообщений в равновероятные случайные контейнерные последовательности по функции встраивания однократная подстановка. Сформированные таким образом стего легко выявляются нарушителем на фоне обычных избыточных сообщений. Однако прочитать эти сообщения принципиально невозможно, если при встраивании используется случайная равновероятно распределенная ключевая последовательность [Шен].

Выражение (4.9) означает, что неопределенность нарушителя относительно сообщения М не должна уменьшаться при знании им стего S и контейнера C , то есть М должно быть независимо от S и С . Исследуем условия стойкости стегосистем. Полагаем, что не только алфавиты S и С , но и их энтропии H ( S ) и H ( С ) равны. Рассмотрим два случая.

1. Пусть никакое сообщение М не встраивается в контейнер С . Очевидно, что в этом случае, коль S и С совпадают, то выполняется H(S/C) = H(C/S) = 0 .

2. В стего S имеется сообщение М с энтропией H ( М ) > 0. Очевидно, что при наличии этой встроенной информации у нарушителя появляется отличная от нуля неопределенность относительно S , если известно С и неопределенность относительно С , если известно S: H ( S/C )) > 0, H ( C/S ) > 0. Следовательно, взаимная информация между скрываемыми сообщениями и соответствующими контейнерами и стего уже не может быть равной нулю:

.

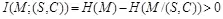Поэтому,

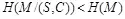. (4.11)

Это означает, что условие стойкости стегосистемы не обеспечивается. Можно показать, что необходимым и достаточным условием стойкости является:

H ( S/C ) = H ( C/S ) = 0. (4.12)

Поэтому в работе [2] делается вывод, что если нарушителю известны стегограммы и соответствующие им контейнеры, то стегосистема не может быть совершенной. В рамках теоретико-информационной модели рассматриваемая стегосистема в атаке нарушителя с известным контейнером не может скрыть факта передачи скрываемого сообщения. А из выражения (4.11) следует, что нарушитель также способен узнать если не полностью, то частично содержание этого сообщения: если 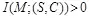, то при известных S и С неопределенность нарушителя об этом сообщении меньше его энтропии.

Обеспечение требуемой стойкости может быть получено при переходе от детерминированных стегосистем к недетерминированным (вероятностным). Рассмотрим один из возможных вариантов построения вероятностной стегосистемы, предложенный в [2]. В рассматриваемой вероятностной стегосистеме для выполнения необходимого и достаточного условия стойкости вида H ( S/C ) = H ( C/S ) = 0 обеспечивается неизвестность для нарушителя используемого контейнера. Для этого в модель стегосистемы вводится источник контейнеров C S , характеристики которого известны нарушителю. Для встраивания скрываемых сообщений из множества C S случайно и равновероятно выберем подмножество контейнеров С , которое назовем подмножеством действительных контейнеров: 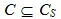. Пусть выполняется условие H ( С S ) >= H ( С ) и вероятностные характеристики подмножества С отличаются от соответствующих характеристик множества C S . Потребуем, чтобы неопределенность нарушителя относительно действительных контейнеров при известном множестве C S была бы строго больше нуля: H ( С/С S ) > 0. Физически это может быть обеспечено, если выбор действительных контейнеров осуществляется с помощью случайного и равновероятного значения R , полученного с выхода генератора случайных чисел, как это показано на рис. 4.2.