Вадим Грибунин - Цифровая стеганография

Необходимая неопределенность относительно С достигается выбором каждого контейнера совершенно случайным образом и сохранением выбора в тайне. Примером такого процесса может быть взятие выборок из аналогового входного сигнала, такого как речь или видео. Погрешность квантователя обеспечивает необходимую неопределенность. Если изменения контейнера в процессе встраивания информации остаются в пределах погрешности квантователя, то такая манипуляция не может быть обнаружена.

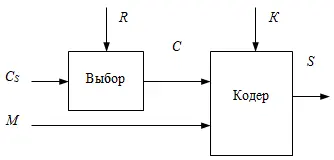
Рис. 4.2. Стегосистема с рандомизированным выбором контейнера

Определим, что для рассматриваемой вероятностной стегосистемы основное условие стойкости выражается в виде

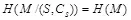. (4.13)

Это означает, что неопределенность нарушителя относительно M не может быть уменьшена знанием S и C S , или M является независимым от S и C S .

Исследуем условия, при которых нарушитель не способен обнаружить изменения в контейнере, произошедшие при встраивании сообщения M с энтропией H ( M ), наблюдая стего. Для этого определим требуемую величину неопределенности нарушителя относительно контейнера H ( C/S ). Можно показать, что

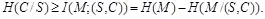(4.14)

При наихудшем случае противник способен полностью определить M из S и C : .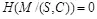

Следовательно, в общем случае выполняется

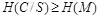. (4.15)

Так как взаимная информация 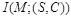не может быть более величины H ( M ), неопределенность 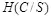должна быть, по крайней мере, той же величины, чтобы сделать чтение сообщения невозможным.

В стойкой стегосистеме, нарушитель, наблюдая стего S , не должен получить информацию сверх той, которая ему известна априори из знания множества C S :

H ( C/C S ) = H ( C/S ), (4.16)

и, поэтому,

H ( C/C S ) >= H ( M ). (4.17)

Таким образом, для нарушителя, знающего характеристики множества C S , в стойкой стегосистеме неопределенность относительно подмножества действительных контейнеров C должна быть не меньше энтропии скрываемых сообщений.

Определим совместную энтропию H 0между множествами C и C S

H 0= H ( C,C S ) = H ( C ) + H ( C S/C ). (4.18)

Так как 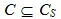и H ( C S ) >= H ( C ), то

H ( C S/C ) >= H ( C/C S ).

Для стойкой стегосистемы получим нижнюю границу величины совместной энтропии

H 0>= H ( C ) + H ( C/C S ).

Используя выражение (4.17), запишем

H 0>= H ( C ) + H ( M ). (4.19)

Так как H ( C S ) >= H ( C ), то H ( C S,S ) >= H ( C,S ). Следовательно,

H ( C S,S ) >= H ( C,S ). (4.20)

В соответствии с выражением (4.15) получим, что граница может быть определена в виде:

H ( C S,S ) >= H ( M ). (4.21)

Сформируем заключение: при достижении нижней границы для H ( C/S ) (уравнение 4.15), нарушитель, знающий S и C S , не способен получить доступ к скрываемому в стего S сообщению M . Фундаментальное условие стойкости (4.13) может быть выполнено.

Рассмотрим условия, при которых нарушитель не способен определить ключ К стегосистемы. Потребуем, чтобы нарушитель, знающий S и C S , не мог получить никакой информации ни о ключе К , ни о сообщении М . Это может быть выражено в виде

I (( K,М );( S,C S )) = H ( K,М ) — H (( K,М )/( S,C S )) = (4.22)

H ( K,М ) — H ( K /( S,C S )) — H ( М/ ( S,C S,K )) = 0.

При знании ключа К , множества C S из стего S однозначно извлекается сообщение М :

H ( М /( S,C S,K )) = 0,

Поэтому из выражения (4.22) получим

H ( K /( S,C S ) = H ( K,М ),

или

H ( K /( S,C S ) = H ( М ) + H ( K/М ) >= H ( М ), (4.23)

соответственно, так как H ( K/М ) >= 0.

Таким образом, для нарушителя неопределенность ключа стойкой стегосистемы должна быть не меньше неопределенности передаваемого скрытого сообщения. Это требование для совершенных стегосистем очень похоже на требование неопределенности ключа К для совершенных систем шифрования, для которых энтропия ключа К при перехваченной криптограмме Е должна быть не меньше энтропии шифруемого сообщения М [7]:

.

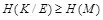Делаем вывод, что действительный контейнер должен быть неизвестным для нарушителя, чтобы обеспечить теоретико-информационную стойкость стегосистемы. Нарушитель не способен ни обнаружить факт передачи скрываемого сообщения, ни читать его, если выполняются два условия:

1) Знание S и C S не уменьшает для нарушителя неопределенности о скрываемом сообщении

H ( М /( S,C S )) = H ( М/S ) = H ( М ).

2) Условная энтропия ключа должна быть не меньше энтропии скрываемого сообщения:

H ( K /( S,C S )) >= H ( М ).

При таких условиях требуемая стойкость может быть обеспечена в вероятностных стегосистемах.

В работе [2] приводятся общие описания возможных вероятностных стегосистем. Пусть отправитель для встраивания скрываемых сообщений в качестве действительных контейнеров использует цифровое изображение пейзажа на выходе электронной камеры. Нарушитель может знать общий вид снимаемого изображения и характеристики используемой камеры. Но атакующий и даже законный получатель не знают точное положение камеры и угол съемки. Колебание камеры даже на долю градуса приводит к существенно отличающимся снимкам. Поэтому при анализе нарушителем перехваченного стего он не способен определить какое цифровое изображение является действительным контейнером и тем самым не может выявить различия между стего и контейнером. В качестве множества контейнеров C Sв данном примере используются всевозможные варианты изображения пейзажа под разными углами с учетом неидеальности оптико-электронного преобразователя используемой камеры.

Вторым примером вероятностной стегосистемы является использование в качестве действительных контейнеров значений отсчетов аналогового случайного сигнала, например, речевого. В различных технических устройствах для преобразования аналоговых сигналов к цифровому виду используются аналого-цифровые преобразователи с некоторой погрешностью квантования отсчетов, причем моменты дискретизации отсчетов определяются тактовым генератором, положение стробирующих импульсов которого также имеет некоторую погрешность. Следовательно, для нарушителя, точно знающего характеристики аналогового сигнала, существует неопределенность между аналоговым и цифровым представлением сигнала. При использовании такого сигнала в качестве контейнера, потенциально можно построить стойкую стегосистему, если энтропия встраиваемого сообщения не превышает величины указанной неопределенности [12].