Вадим Грибунин - Цифровая стеганография

.

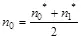Зная общее число n появления всех элементов исследуемой последовательности, легко подсчитать ожидаемую вероятность появления этих элементов в стего по правилу: 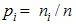. Соответственно, для исследуемой последовательности вероятности равны: .

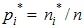Величина Хи-квадрат для сравниваемых распределения исследуемой последовательности и ожидаемого распределения стего равна

,

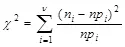где v есть число степеней свободы. Число степеней свободы равно числу k минус число независимых условий, наложенных на вероятности 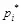. Наложим одно условие вида

.

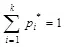Вероятность p того, что два распределения одинаковы, определяется как

p ,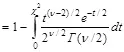

где Г есть гамма-функция Эйлера.

Чем больше значение p, тем выше вероятность встраивания скрываемой информации в исследуемую последовательность.

Рассмотрим использование критерия Хи-квадрат для отыскания следов стегоканала, образованного с использованием программы EzStego. Пусть в контейнерное изображение «Мельница», показанное в левой части рис. 4.3, в НЗБ спектральных коэффициентов изображения, начиная с его верхнего края до его середины, последовательно внедрено 3600 байт скрываемого сообщения. На рис. 4.6 показана вероятность встраивания скрываемой информации в зависимости от размера исследуемой последовательности. Начало графика получено при анализе первого фрагмента стего, составляющего одну сотую часть всего стего. Значение p составило 0,8826. Затем к анализируемому фрагменту была добавлена еще одна сотая часть стего, и так далее. На втором шаге вероятность составила 0,9808 и далее при анализе стего не опускалась ниже 0,77. При переходе к анализу нижней части части изображения, не содержащей скрываемой информации, величина p скачком уменьшилась до нуля.

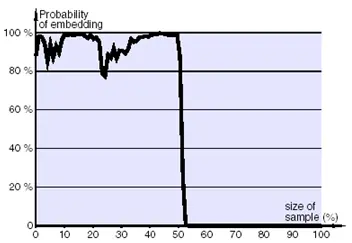
Рис. 4.6. Вероятность встраивания по критерию Хи-квадрат при анализе EzStego

В программе Steganos встраиваемое двоичное сообщение любой длины дополняется до длины контейнера (до числа пикселов изображения). Поэтому критерий Хи-квадрат при встраивании сколь угодно малого сообщения с использованием Steganos дает вероятность существования стегоканала, практически не отличающуюся от единицы.

В программе S-Tools встраиваемое сообщение равномерно распределяется по всему контейнеру. При полностью заполненном контейнере по критерию Хи-квадрат уверенно выявляются следы вложения посторонней информации с пренебрежимо малой вероятностью ошибки (менее 10 -16), но при заполненном контейнере на треть и менее следы стегоканала не выявляются.

Как и в EzStego, в программе Jsteg скрываемое сообщение последовательно встраивается в коэффициенты преобразования контейнера. На рис. 4.7 показана вероятность встраивания по критерию Хи-квадрат при анализе стего, сформированной с использованием Jsteg. Видно, что статистическая атака успешно обнаруживает следы скрываемой информации в первой части исследуемой последовательности, содержащей скрываемое сообщение, и не дает ложной тревоги во второй ее части, являющейся пустым контейнером.

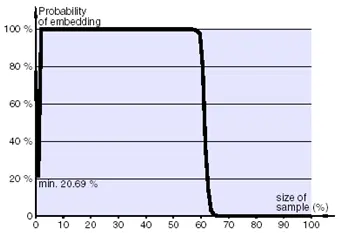
Рис. 4.7. Вероятность встраивания по критерию Хи-квадрат при анализе Jsteg

Для сжатия изображений очень часто используется алгоритм JPEG. На рис. 4.8 показано, что вероятность ложного срабатывания по критерию Хи-квадрат при анализе пустых контейнеров, сжатых алгоритмом JPEG, не превышает пренебрежимо малой величины 0,407 %.

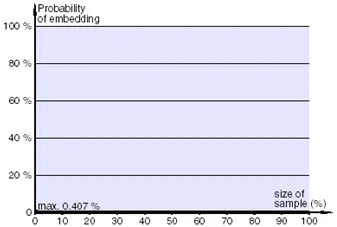
Рис. 4.8. Вероятность ложного срабатывания по критерию Хи-квадрат при сжатии по JPEG пустого контейнера

Рассмотрим статистические атаки, разработанные с целью обнаружения скрытых каналов передачи информации в аудиофайлах. В работе [16] показано, что следы скрытия проявляются при анализе таких статистических характеристик речи и музыки, как распределение НЗБ отсчетов, условные распределения младших и остальных разрядов отсчетов, величины коэффициента корреляции между соседними отсчетами и т. п.

Было исследовано более 1200 аудиофайлов, записанных на CD-дисках и представляющих собой различные музыкальные и вокальные произведения разных авторов. Показано, что для пустых аудиоконтейнеров НЗБ и остальные биты статистически взаимно зависимы, причем на характер этой зависимости влияет уровень записи (усредненная амплитуда отсчетов аудиосигнала). На рис. 4.9 показана полученная для аудиофайлов зависимость статистики Хи-квадрат. По критерию Хи-квадрат вычислялась степень различия между распределением пустых и заполненных контейнеров от характерного для стего бернуллиевского распределения.

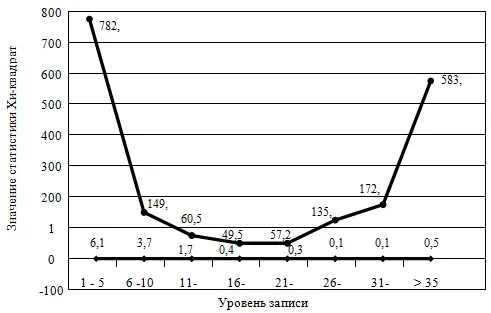
Рис. 4.9. Зависимость величины Хи-квадрат от амплитуды отсчетов аудиосигнала:

— аудиоконтейнер;

— стего

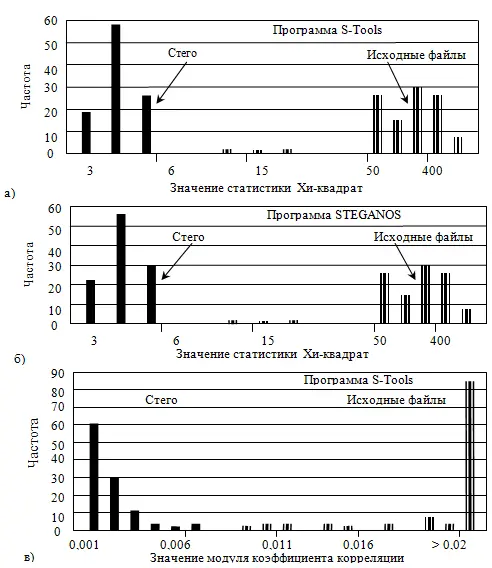
Рис. 4.10. Статистические различия стего и пустых аудиоконтейнеров: а, б — по критерию Хи-квадрат, в — по модулю коэффициента корреляции

К настоящему времени известны различные программные средства скрытия информации в аудиофайлах. Используя статистику Хи-квадрат и коэффициент корреляции, в работе [16] проведен стегоанализ программ Steganos (version 1.0а) и S-Tools (Steganography Tools for Windows, version 4.0), которые скрывают информацию в наименее значимых битах звуковых отсчетов. В качестве исходных контейнеров исследовались считанные с CD-дисков 100 музыкальных фрагментов различных исполнителей длительностью звучания 15 секунд каждый (как со стандартных музыкальных компакт-дисков, так и с дисков в формате МРЗ). В качестве скрываемого сообщения использовалась псевдослучайная последовательность объемом 83 Кбайт и побитно внедрялась в каждый НЗБ контейнера. По критерию Хи-квадрат определялась степень отличия распределения НЗБ отсчетов исследуемой последовательности от от бернуллиевского распределения.