Вадим Грибунин - Цифровая стеганография

Атака (игра) заключается в следующем. Нарушитель имеет неоднократную возможность генерировать контейнеры и соответствующие им стего, пытаясь выяснить структуру стегоалгоритма. При этом имеется то ограничение, что вся процедура должна быть полиномиальной по длине ключа и размеру контейнера. После того, как он закончил работу, ему предъявляются два случайно выбранных контейнера: один пустой, другой — заполненный. Стегосистема называется условно стойкой, если у нарушителя нет возможности правильного определения стего с вероятностью, незначительно отличающейся от 1/2. В работе [20] дано определение понятия «незначительно отличающейся» и приведено математическое описание вербально изложенной выше модели. Условно стойкая стегосистема сохраняет это свойство для всех возможных ключей и всех возможных контейнеров.

Ясно, что понятие условно стойкой стегосистемы более слабое, чем понятие стегосистемы, стойкой с информационо-теоретической точки зрения и включает ее как частный случай. Безусловно стойкая стегосистема в приведенной выше модели получается в случае, если снять ограничение полиномиальности во времени игры.

Каким образом построить условно стойкую стегосистему? Одна из возможностей, широко используемая и в криптографии, заключается во взятии за основу какой-нибудь трудной в вычислительном смысле математической задачи, например, обращение односторонней функции (разложение на множители, дискретное логарифмирование и т. д.). Тогда останется показать связь между невозможностью решения этой задачи и невозможностью вскрытия стегосистемы — и условно стойкая стегосистема построена. Из криптографии известно, что, к сожалению, вопрос построения доказуемо односторонней функции нерешен. В работе [20] показано, как можно построить стегосистему на основе известного криптоалгоритма RSA.

Ранее была исследована стойкость стегосистем к попыткам пассивного нарушителя установления факта скрытия передаваемых сообщений. Дополнительно к требованиям скрытности связи могут предъявляться требования по исключению навязывания в стегоканале ложных сообщений активным нарушителем. Например, в работе Г.Симмонса описана так называемая задача заключенных [6]. В этой задаче арестованные Алиса и Боб пытаются по скрытому каналу связи договориться о побеге. Тюремщик Вилли пытается не только обнаружить факт обмена информации, но и от имени Алисы навязать Бобу ложную информацию. Потому рассмотрим особенности построения стегосистем с возможностью аутентификации передаваемых сообщений, возможные атаки нарушителя и определим оценки имитостойкости стегосистем.

Формально опишем построение стегосистемы с аутентификацией скрытно передаваемых сообщений. Пусть стегосистема использует секретный ключ, принимающий значения 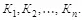Множество контейнеров С разбивается на n подмножеств 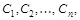каждое из которых описывается своим вероятностным распределением 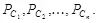Поставим подмножества 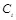контейнеров в соответствие секретным ключам 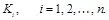При действующем ключе аутентификации 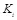сообщение, доставленное по каналу скрытой связи, считается получателем подлинным, если оно вложено в контейнер, принадлежащий подмножеству с распределением 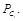Если при действующем ключе 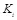заполненный контейнер не принадлежит подмножеству 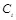, то извлеченное из него сообщение признается получателем ложным. Таким образом, при действующем ключе все множество контейнеров разделено на допустимые, в которых подлинность вложенных в них сообщений признается получателем, и недопустимые, которые не могут быть выбраны для передачи отправителем скрываемых сообщений. Следовательно, получение таких контейнеров с вложенными сообщениями означает, что они навязаны нарушителем.

Если принятое стего S имеет распределение 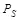, совпадающее с распределением 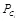множества допустимых контейнеров при действующем ключе 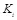, то функция проверки подлинности скрываемых в них сообщений 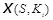принимает единичное значение и полученное сообщение признается подлинным, а если распределения не совпадают, то функция принимает нулевое значение и сообщение отвергается как имитонавязанное:

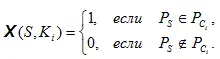
Функция проверки подлинности при построении стегосистемы с аутентификацией сообщений может быть задана аналитически, графически или в виде таблицы. При аналитическом задании каждому значению ключа ставится в соответствие свое подмножество допустимых контейнеров. Эти подмножества отличаются друг от друга законами распределения или их параметрами. Например, используются различные распределения вероятностей непрерывных контейнеров (нормальное, Райса, Накагами и другие). Или подмножества контейнеров-изображений отличаются спектральными характеристиками. Например, в каждом подмножестве энергия спектра изображений сосредоточена в своем диапазоне частот. Известно, что изображения можно разделить на высокочастотные, основная энергия спектра которых принадлежит верхней полосе частот, и на низкочастотные. Также можно разделить контейнеры-изображения на подмножества по типу сюжета: пейзаж, портрет, натюрморт и т. п. Хотя при сюжетном разбиении трудно математически строго задать функцию 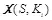в терминах законов распределения, на практике задание такой функции не представляет труда. Множество всех контейнеров разбивается на n непересекающихся подмножеств контейнеров 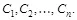Например, контейнеры могут быть разбиты на подмножества их пересечением. При действующем ключе 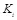отправитель выбирает подмножество контейнеров 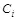. Скрываемое сообщени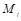е , где 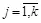, встраивается в контейнер этого подмножества, образуя стегограмму 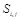. Получатель стегограммы проверяет ее соответствие действующему ключу. Он убеждается, что полученная стегограмма допустима при ключе 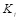, если выполняется 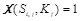. Это равенство выполняется, если стегограмма 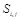принадлежит подмножеству контейнеров 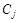. Следовательно, извлеченное из этой стегограммы сообщение 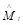подлинно. Но если принятая стегограмма не принадлежит допустимому подмножеству контейнеров, то функция проверки принимает нулевое значение, и принятое сообщение 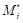отвергается как ложное. Графическое описание функции проверки подлинности представлено на рис. 4.12. Пусть по стегоканалу могут передаваться k различных сообщений: 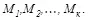Множество ключей стегосистемы состоит из n ключей, из которых равновероятно и случайно выбирается действующий ключ.