Владо Дамьяновски - CCTV. Библия видеонаблюдения. Цифровые и сетевые технологии

Допустим, встроенный экспонометр моего фотоаппарата показывает выдержку 1/15 с и диафрагму F-2.8. В фотоаппарат заряжена фотопленка с чувствительностью 100 единиц ISO. В результате мы получаем экспозиционное число:

EV (F-2.8+1/15)= 6.7∙lg(2.8) — 3.32∙lg(1/15) = 3 + 4 = 7

Что даст нам освещенность

Iлк = 2.5∙2 7= 320лк

Чтобы перевести это значение в фут-канделы, нужно разделить его на 10, что даст нам приблизительно 32 фут-канделы.

Большинство из нас, вероятно, знают, что в солнечный день уровень освещенности составляет примерно 100,000 лк, в обычном офисе — примерно от 100 до 1000 лк, а лунной ночью — около 0.1 лк и т. д.

В яркий солнечный день мы получим экспозиционное число порядка 15–16, тогда как для видеонаблюдения ночью при нормальном уличном освещении экспозиционное число будет 3, что при переводе даст нам 20 лк.

Не забывайте об ограниченном диапазоне измерений экспозиционного числа. У большинства фотоаппаратов диапазон измерений экспозиционного числа лежит в интервале от 1 до 20. Это означает, что самый низкий уровень освещенности, который вы сможете измерить таким фотоаппаратом, равен 5 лк. Этого будет вполне достаточно при проектировании большинства систем видеонаблюдения, но если вам необходимо измерить и более низкие уровни освещенности, то я рекомендую приобрести профессиональный люксметр или фотоэкспонометр.

Чтобы как следует себе представить «световой вопрос» с точки зрения камеры, нам нужно знать, какое количество света действительно падает на фотоприемник.

Величина освещенности на ПЗС-матрице (ИС на ПЗС) (или лицевой панели) Е пзсв первую очередь зависит от яркости объекта L, а также от F-числа, т. е. собирающей способности линзы. Чем ниже F-число, тем больше света проходит через объектив (ниже мы еще рассмотрим этот вопрос). Эта величина также пропорциональна коэффициенту пропускания объектива т. А именно, в зависимости от качества стекла и производителя, а также от механики внутренних поверхностей, определенный процент света теряется в самом объективе.

Все вышеупомянутые факторы можно представить следующим соотношением:

Е пзс= L∙τ∙π/4∙F 2)[лк] (11)

Ниже мы покажем, как выводится это соотношение, чтобы люди, используя эти формулы, могли четко понимать, что здесь предполагается, а что аппроксимируется (11). Но поскольку для этого требуются более сложные математические выкладки, то читатели, не испытывающие к этому интерес или не имеющие соответствующей базы, могут просто воспользоваться соотношением (11) как оно есть, помня при этом, что L — это средняя яркость объекта (в люксах), — это коэффициент пропускания объектива (в процентах), F— это F-число и равно 3.14.

Объект, находящийся в поле зрения камеры и освещенный источником света, испускает свет практически во всех направлениях, в зависимости от функции отражения. На практике объект с гладкими поверхностями в большинстве случаев может считаться ламбертовской равномерно рассеивающей поверхностью.

Тогда можно рассматривать поток, проходящий через полусферу радиуса rс центром ds. Пусть dθ— это приращение угла θк нормали, тогда поток в объеме, образованном вращением угла dθпроходит через окружность на поверхности сферы, причем радиус окружности равен r dθ, длина — 2π∙r 2∙sinθ∙dθ.

Рис. 2.10. Ламбертовская рассеивающая поверхность

Эта элементарная площадка на поверхности сферы задается следующим соотношением:

dA= 2π∙r 2∙sinθ∙dθ(12) и тогда телесный угол ω, стягиваемый конусом в центре сферы, задается соотношением:

ω= dA/r 2= 2π∙r 2∙sinθ∙dθ/r 2= 2π∙sinθ∙dθ[стерадиан] (13)

поскольку сила света на ламбертовской поверхности (поток в стерадиане) в заданном направлении пропорциональна косинусу угла к нормали, а сила света полной поверхности в направлении нормали равна I, то под углом θ она будет равна I∙cosθ

Сила света dIэлементарной площадки dsравна:

dI = I∙cosθ∙ds /s[люмен/стерадиан = кандел] (14)

поскольку I/sэто действительная освещенность Lв перпендикулярном направлении, то вышеприведенное соотношение принимает вид:

dI = L∙ cosθ∙ds [кд] (15)

Элементарный поток dFравен элементарной силе света dI, помноженной на телесный угол:

dF= L∙ cosθ∙ds∙2π∙sinθ∙dθ [лм] (16)

Общий поток в конусе, образованном углом θможно найти интегрированием от 0 до θ:

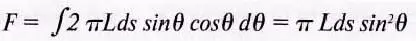
[лм] (17)

Если мы хотим найти полный световой поток, испускаемый во всех направлениях, то нужно положить угол θравным 90°, тогда получим:

F t= L∙π∙ds[лм] (18)

Теперь, если нам надо сосчитать поток в телесном угле, меньшем 90°, как это происходит в случае, когда камера направлена на объект, общий поток F t задается формулой:

F 0 = π∙L∙ds 0∙sin 2θ 0[лм] (19)

Если коэффициент пропускания линзы равен τ, то поток, падающий на плоскость ПЗС (или лицевую панель), равен:

F ПЗС= F 0∙τ = τ∙π∙L∙ds 0∙sin 2θ 0

Освещенность ПЗС-матрицы (или лицевой панели) будет равна потоку, деленному на площадь, т. е.

E ПЗС= τ∙π∙L∙ds 0∙sin 2θ 0/ds ПЗС[лк] (21)

Рис. 2.11. Вычисление светового излучения с помощью ламбертовской рассеивающей поверхности

Отношение (ds ПЗС/ds 0), обратное которому использовалось в предыдущей формуле, известно как коэффициент увеличения объектива m. Коэффициент увеличения может быть также аппроксимирован как отношение между фокусным расстоянием линзы и расстоянием от линзы до объекта

m = (f/D) 2= ds ПЗС/ds 0 (22)

Когда мы произведем подстановку этих отношений в нашу основную формулу, то получим:

E ПЗС = π∙τ∙L∙sin 2θ 0∙(D/f) 2[лк] (23)

Здесь потребуется ввести еще одно отношение, связанное с объективом (d/f), которое также известно как F-число объектива. Для объектов, которые расположены достаточно далеко от телекамеры (а это типично в большинстве случаев для систем видеонаблюдения) будет справедливо следующее:

tgθ 0= d/2D = sinθ 0/cosθ 0= sinθ 0(24)

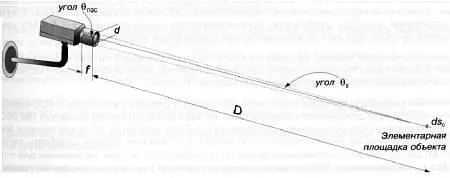
Рис. 2.12 . Вычисление количества света, падающего на ПЗС-матрицу

Такое допущение имеет право на существование, потому что для очень больших расстояний до объекта угол θ 0будет крайне мал, а значение косинуса этого угла будет стремиться к 1.