Евгений Айсберг - Радио?.. Это очень просто!

Л. — Это совершенно верно. Но если бы каждый передатчик занимал в пространстве полосу частот 20 кгц, то не хватило бы места для размещения необходимого числа передатчиков. По международному соглашению, за исключением коротких волн, где больше свободы, ширину боковых полос ограничили 4,5 кгц.

Таким образом, каждый передатчик занимает полосу частот 9 кгц. Это как раз и дает возможность получить между двумя несущими частотами разнос в 9 кгц для того, чтобы два передатчика не мешали друг другу (рис. 110) при условии, конечно, что приемник будет иметь избирательность, достаточную для разделения 9 кгц.

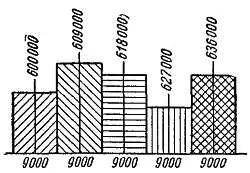
Рис. 110. Спектры частот передатчиков. Несущие частоты разнесены на 9 кгц. Модулирующие частоты не превышают 4,5 кгц.

Н. — Я думаю, что, имея достаточное количество настроенных контуров, можно сделать такой приемник, который принимал бы колебания только одной частоты.

Л. — Это было бы напрасной тратой времени! Отдаешь ли ты себе отчет, Незнайкин, что такой приемник мог бы принимать всего одну какую-нибудь ноту. Разве можно испытать удовольствие от исполнения, например Пасторальной симфонии, если из всего богатства звуков ты услышишь только ми-бемоль третьей октавы?

Н. — Конечно, нет. Я вижу, что приемник должен пропустить без искажений всю полосу боковых частот 9 кгц, чтобы воспроизвести всю гамму передаваемых звуков.

Л. — Нo нельзя, чтобы он пропускал более широкую полосу частот. Иначе возникнут помехи из-за биений с частотами соседних станций. И вот ты перед лицом этой ужасной дилеммы, которая противопоставляет качество передачи и избирательность: чем меньше избирательность, тем выше качество воспроизведения.

Н. — Если уж выбирать между избирательностью и качеством звучания, то я высказываюсь за второе.

Л. — К чему добиваться правильного воспроизведения всех частот, если эту передачу будет покрывать свист помехи?

Н. — Но разве не существует возможности полностью пропустить полосу 9 кгц и не пропустить больше ничего другого вне этой полосы?

Л. — Да, по крайней мере с достаточным приближением. Однако осуществить это при помощи одиночного колебательного контура нельзя. Его резонансная кривая …

Н. — Что это такое? Ты никогда об этом не говорил.

Л. — Так называют кривую, которая показывает, как изменяется в колебательном контуре интенсивность колебаний в зависимости от частоты. Очевидно, что наибольшая амплитуда колебаний в контуре будет в момент резонанса. По мере изменения частоты интенсивность колебаний в контуре более или менее резко падает в зависимости от сопротивления контура по высокой частоте.

Если контур имеет большое сопротивление или, как говорят, обладает большим затуханием, то его резонансная кривая будет иметь более пологую форму (рис. 111) и сможет пропустить большую полосу частот. Но наряду с этим он будет и малоизбирательным.

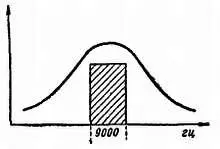
Рис. 111. Резонансная кривая контура с большим затуханием; плохая избирательность — хорошее качество воспроизведения.

Если, наоборот, контур имеет очень малое затухание (рис. 112), то он пропускает только узкую полосу частот. При высокой избирательности он не пропустит всю совокупность боковых частот. Идеальная резонансная кривая должна была бы иметь форму прямоугольника с шириной 9 кгц. Контур с такой кривой пропускал бы полосу частот только в 9 кгц и ничего другого.

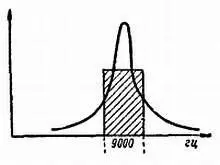
Рис. 112. Контур с малым затуханием; хорошая избирательность — плохое качество воспроизведения.

Н. — Если ты говоришь, что такая кривая является идеальной, значит ее невозможно получить?

Л. — Да, но к ней можно приблизиться с помощью так называемых полосовых фильтров .

Простейшие полосовые фильтры состоят из двух связанных между собой колебательных контуров с малым затуханием, настроенных на несущую частоту. Путем изменения связи между ними можно получить более или менее широкую резонансную кривую, по форме приближающуюся к прямоугольной (рис. 113).

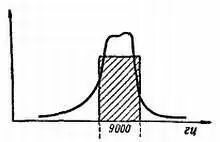
Рис. 113. Резонансная характеристика полосового фильтра, сочетающая хорошую избирательность с хорошим качеством воспроизведения.

Н. — А как осуществить связь между двумя колебательными контурами, составляющими полосовой фильтр?

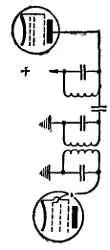
Л. — Самый простой способ — соединить их индуктивно, что и является трансформатором с настроенными первичной и вторичной обмотками (рис. 114), или осуществить связь при по мощи конденсатора малой емкости (рис. 115). В более сложных фильтрах связь осуществляется через реактивное сопротивление (рис. 116).

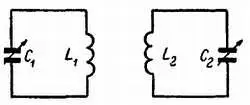
Рис. 114. Полосовой фильтр с индуктивной связью .

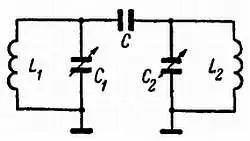
Рис. 115. Фильтр с емкостной связью.

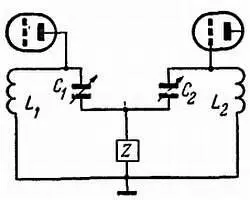
Рис. 116. Фильтр со связью через общее реактивное сопротивление Z.

Н. — Каким же образом общее сопротивление может служить элементом связи?

Л. — Ток, протекающий в первом контуре, создает на этом сопротивлении падение напряжения, которое приложено ко второму контуру и возбуждает в нем ток. Если сопротивление мало, то и развиваемое на нем напряжение будет малым, что равноценно слабой связи.