Владимир Внуков - Артиллерия

Немного позади окопов виднеется деревня (рис. 173). Ничто не говорит о том, что в ней имеются войска. Но вы можете не сомневаться, что в деревне расположены и пехота, и ее огневые средства (пулеметы, батальонная артиллерия).

Километрах в двух за окопами находится лес – наибольшее препятствие для наблюдения. Разгадать, что творится в лесу, – задача почти неразрешимая, и не только для наземной, но, если лес густой и к тому же лиственный, и для воздушной разведки. Из этого, конечно, не следует, что за лесом вообще не стоит наблюдать. Тщательное наблюдение за лесными опушками, за дорогами и тропинками, ведущими в лес, все же поможет вам разгадать, что скрывается в этом лесу: резервы пехоты, танки, может быть, артиллерия.

Немного правее леса вы видите заросли кустарника. Хотя кустарник и не в такой мере, как лес, маскирует расположение противника, но и в нем могут быть скрыты важные для нас цели: пулеметы, противотанковые пушки, пехота. Изучать кустарник надо так же тщательно, как и лес.

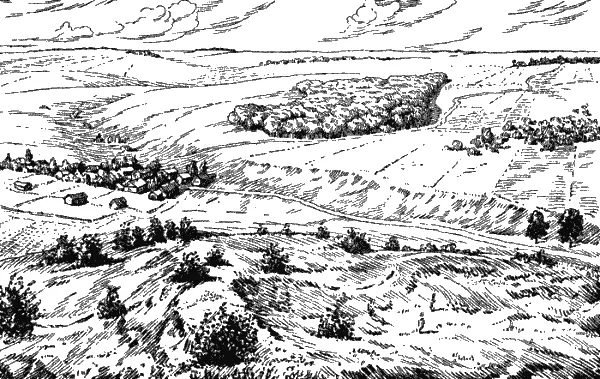
Рис. 173. Вот что видите вы с наблюдательного пункта

Еще правее и дальше вы видите опять деревню. В деревне, расположенной в ближайшем тылу противника, могут находиться его резервы, склады, артиллерийские парки и тому подобное. Непосредственно за населенным пунктом можно обнаружить иногда артиллерийскую позицию, для которой дома и сады будут служить укрытием. Поэтому надо вести наблюдение не только за населенным пунктом, но и за прилегающей к нему местностью.

Цель найдена. Теперь нужно определить ее местоположение, нужно точно вычислить расстояние до цели, чтобы наша артиллерия знала, куда направить свои выстрелы.

Как же это сделать?

Местоположение цели определяется обычно по отношению к ориентиру, – именно, по отношению к тому ориентиру, который находится всего ближе к цели. Достаточно знать две координаты цели – ее дальность, то-есть расстояние от наблюдателя или от орудия до цели, и угол, на который цель видна нам правее или левее ориентира, – и тогда местоположение цели будет определено вполне точно.

Предположим, ради простоты, что цель находится от нас на том же расстоянии, что и ориентир. Расстояние до ориентира нам, конечно, известно заранее: мы потому и называем предмет ориентиром, что местоположение его нам уже известно. Пусть расстояние до ориентира равно 1000 метров. Одна координата цели, следовательно, уже определена. Остается определить другую: угол между целью и ориентиром, – насколько цель видна нам правее или левее ориентира.

Чем же и как артиллеристы измеряют углы? В обыденной жизни вам не раз приходилось измерять углы: вы измеряли их в градусах и минутах. Артиллеристам же приходится не только измерять углы, но и быстро в уме переводить полученные угловые величины в линейные и наоборот. Поэтому измерение углов градусами и минутами для артиллеристов неудобно. Артиллеристы придумали совсем иную меру углов. Мера эта – «тысячная», или, как ее называют иначе, «деление угломера». Представьте себе окружность, разделенную на 6 000 равных частей. Примем за основную меру для измерения углов одну шеститысячную долю этой окружности и попробуем определить ее величину в долях радиуса.

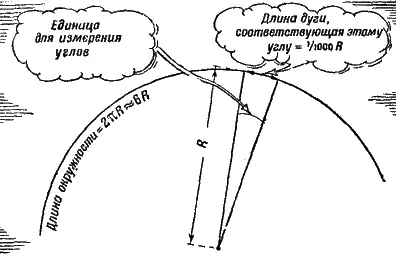
Рис. 174. В артиллерии углы измеряют «тысячными»

Длина любой окружности превосходит, как известно, длину ее радиуса приблизительно в шесть раз. Значит, одна шеститысячная часть окружности – та мера, которой мы решили измерять углы, – будет равна примерно одной тысячной радиуса окружности… Поэтому-то артиллерийская мера углов и носит название «тысячной» (рис. 174). Этой мерой измерять углы очень удобно. Вы убедитесь в этом сами на следующих двух примерах.

Пример первый (рис. 175). Вы определяете угол, под которым видны с вашего наблюдательного пункта пулемет противника и отдельно стоящая сосна. Угол этот равен, оказывается, ста «тысячным». И пулемет, и сосна расположены на одинаковом от вас расстоянии-на расстоянии 2000 метров. Вас интересует, поразят ли осколки 152-миллиметровой гранаты людей у пулемета, если граната разорвется около сосны. Для этого, очевидно, надо прежде всего знать, как же велико расстояние от сосны до пулемета, если его измерять не в угловых, а в линейных величинах, то-есть в метрах.

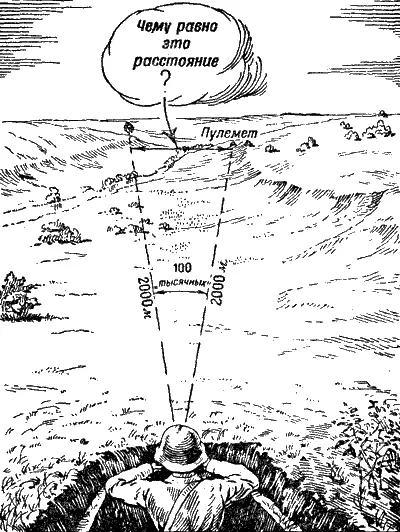
Рис. 175. Как по углу определить расстояние от цели до ориентира

Задача эта решается очень просто. Надо только представить себе, что ваш наблюдательный пункт – это центр той окружности, которая описана радиусом, равным расстоянию от вас до пулемета (или до сосны). Радиус, таким образом, будет равен 2 000 метров. Углу в одну «тысячную» соответствует, как вы знаете, расстояние, равное одной тысячной радиуса, то-есть в данном случае 2 метрам. А так как угол между пулеметом и сосной равен не одной, а ста «тысячным», то, значит, расстояние между пулеметом и сосной равно не 2 метрам, а 200 метрам.

Мы знаем, что действительное поражение осколки 152-миллиметровой гранаты наносят на расстоянии до 35 метров от точки разрыва (рис. 73). Значит, в данном случае нельзя рассчитывать на поражение пулеметчиков осколками гранаты, рвущейся у сосны.

Еще один пример (рис. 176). В канаве около шоссе вы обнаружили группу стрелков, по которой и решили открыть огонь. Вам надо вычислить расстояние до стрелков или, что то же, до шоссе.

Для решения этой задачи воспользуйтесь телеграфными столбами на шоссе; высота их известна – она равна 6 метрам.

Измерьте теперь угол, которым покрывается высота телеграфного столба, и вы будете иметь все данные для решения этой задачи. Допустим, что угол этот оказался равным 3 «тысячным». Но если 6 метрам соответствует с этого расстояния угол в 3 «тысячных», то 1 «тысячной» будут соответствовать 2 метра. А всему радиусу, то-есть расстоянию от вас до шоссе, будет соответствовать величина, в 1 000 раз большая. Нетрудно сообразить, что расстояние от вас до шоссе будет равно 2 000 метров.

В действительности не все расстояния будут выражаться такими числами, как 2 000, 3 000 метров. Числа могут и не оканчиваться нулями. Но принятая в артиллерии мера для измерения углов позволяет, как в этом вы уже убедились, без всякого труда быстро находить одну «тысячную» от любого из таких чисел. Для этого надо только мысленно отделить в таком числе справа три знака, и вы получите значение одной «тысячной» этого числа. Все это проделывается очень быстро в уме.