Сергей Попов - Все формулы мира

Предположим, наш объект поглощает все падающее на него излучение (что не совсем точно). Представьте себе концентрические сферы распространения излучения вокруг звезды, начиная с ее радиуса. Разумеется, через каждую сферу проходит одинаковая энергия, т. е. мы можем себе представить, что поверхность звезды испустила какую-то энергию. Затем всю ее поглотила следующая сфера, после чего переизлучила ту же самую энергию дальше. При этом каждая сфера, начиная с поверхности, испускает тепловое излучение. Тогда для их светимости есть простая формула, которую мы уже использовали выше в других приложениях:

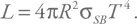
Напомним, что здесь L – светимость, T – температура, R – радиус сферы.

Чем дальше мы отдаляемся от звезды, тем ниже температура сферы, а значит, и каждого ее элемента. Следовательно, меньше будет и температура маленького поглощающего излучение объекта. Нам надо найти расстояние, на котором температура упадет до величины, соответствующей замерзанию воды [134] На всякий случай напомню, что в протопланетном диске не может быть жидкости, так как давление мало. Поэтому из твердого состояния совершается переход сразу в газ, и наоборот. .

Обозначив температуру поверхности звезды T *, а ее радиус – R *, получим:

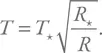
Можем выполнить упражнение: подставим в формулу температуру и радиус Солнца (5800К и 696 000 км) и получим, что 273К (около ноля по Цельсию) достигается примерно на расстоянии 2 а.е. Параметры молодого Солнца отличались от теперешних, но качественно оценка остается верной: для звезд, похожих на молодое Солнце, снеговые линии находятся (для разных веществ) на расстоянии от 2 до 4 а.е. Соответственно, сразу за снеговой линией должно идти активное формирование планет, потому что там и ледяная пыль уже есть, и плотность вещества еще высока (она уменьшается с удалением от звезды).

Именно за снеговой линией формируются планеты-гиганты. Их ядра успевают быстро набрать массу около 10 земных, и тогда начинается быстрый процесс захвата газа из диска (надо торопиться, звезда своим ультрафиолетовым излучением испаряет диск). А внутри снеговой линии рост планетезималей идет медленнее, да и доступного вещества меньше, поэтому достичь критической массы для начала превращения в газовый гигант не удается. В итоге в Солнечной системе внутри снеговой линии мы видим Меркурий, Венеру, Землю и Марс, а за ней – массивные планеты-гиганты. Приятно, что планеты земного типа образуются как раз в зоне обитаемости! Таким образом, в Солнечной системе мы не видим противоречий с описанным выше сценарием.

Но одно дело – объяснять формирование единственной системы (пусть и очень хорошо изученной), и совсем другое – увязать в целостную картину не только весь комплекс данных по экзопланетам, протопланетным дискам и их звездам, но и наше теоретическое понимание процессов, ответственных за формирование и раннюю эволюцию планетных систем. Сделать это можно только с помощью популяционного синтеза, позволяющего сравнивать созданный нами в компьютере искусственный идеальный мир с миром реальным со всеми его «шероховатостями».

Задача о падении тела позволяет на достаточно простом примере продемонстрировать, как мы можем улучшать результаты с помощью расчетов на основе все более точных моделей. Мы последовательно рассмотрим три задачи: падение вблизи поверхности Земли в пренебрежении сопротивлением воздуха, падение с очень большой высоты, падение с учетом сопротивления среды.

Первый вариант задачи совсем школьный – движение с постоянным ускорением. Ускорение создается силой земного притяжения и равно:

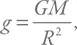
где G – гравитационная постоянная, а M и R – масса и радиус Земли. Тело падает с небольшой высоты h , которая намного меньше R , а потому изменением ускорения можно пренебречь.

Все необходимые формулы приведены в учебнике физики за 9-й класс. За время t скорость будет возрастать на величину gt . При нулевой начальной скорости за время t тело проходит расстояние, равное gt 2/ 2. Откуда берется такая формула, легко представить графически.

Нарисуем график зависимости скорости от времени для равноускоренного движения. Это будет прямая линия. Путь, пройденный за небольшой промежуток времени dt , равен произведению текущей скорости (за маленький интервал времени она не успевает существенно измениться) на dt . Эта величина равна площади вытянутого в вертикальном направлении прямоугольника на графике. Соответственно, весь пройденный путь складывается из суммы таких прямоугольников и, таким образом, равен площади фигуры под линией изменения скорости, представляющей собой треугольник. Его площадь можно вычислить: умножим половину длины стороны на высоту треугольника, опущенную к этой стороне. Сторона равна t , а высота – это конечная скорость, равная gt . Соответственно, время падения с высоты h равно квадратному корню из удвоенной высоты, разделенной на ускорение свободного падения: t = (2 h / g ) 1 / 2.

Теперь рассмотрим более сложный случай – падение с большой высоты, сравнимой с радиусом Земли. В такой постановке ускорение будет меняться, т. е. скорость будет расти все быстрее. Подобный эксперимент можно было бы поставить на Луне, где не мешает атмосфера.

Мы не будем решать задачу до конца путем интегрирования (хотя интеграл там табличный), но зато получим качественную зависимость времени падения от начального радиуса для случая, когда он намного больше радиуса планеты R . Очевидно, что чем дальше мы отходим от поверхности, тем меньше ускорение: a ( r ) = GM / r 2, где r = R + h .

Значит, если мы рассмотрим небольшой интервал времени dt , в течение которого смещение невелико и ускорение меняется слабо, то dr = v ( r ) dt + a ( r ) ( dt ) 2/ 2. Полное время падения с расстояния r будет в основном определяться медленным движением вдали от планеты: там и скорость еще мала, и ускорение невелико. Значит, верхним пределом на время падения будет величина, которую можно получить из уже записанной формулы t = (2 h / g ) 1 / 2. Заменим здесь высоту h на r , а ускорение g – на соответствующую величину a ( r ) = GM / r 2. В итоге мы получим, что при больших расстояниях от поверхности время падения растет как r 3 / 2.

Неплохой оценкой времени падения является отношение начального расстояния r к скорости свободного падения на этом расстоянии: v = (2 GM / r ) 1 / 2. Иными словами, 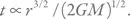Такую оценку часто применяют, например, для определения времени падения захваченного из межзвездной среды вещества на нейтронную звезду. Разумеется, точная величина будет несколько меньше, но по порядку величины это очень хорошая простая оценка.