Райан Норт - Как изобрести все. Создай цивилизацию с нуля

Что произойдет, если заменить «истинно» на «1», а ложно на «0»?

Ну, у вас есть таблица истинности для p и ¬p, которая выглядит подобным образом (табл. 19)…

Таблица 19.Таблица истинности для p и ¬p

…и которую можно превратить в список ожидаемых входных и выходных состояний бинарной машины – мы называем их «ячейками», – выглядящий следующим образом (табл. 20).

Таблица 20.Узрите же, ибо это первое в мире представление НЕТ-ячейки

Любая машина, получившая определенное значение на входе, выдаст столь же определенное значение на выходе. И совершенно не важно, как этот результат будет получен, что происходит внутри, главное, что она функционирует как НЕТ-ячейка: 1 на входе значит 0 на выходе и наоборот.

Ее можно даже нарисовать в виде схемы (рис. 62).

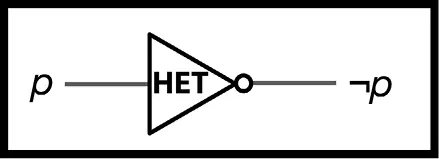
Рис. 62.Представление НЕТ-ячейки в графическом виде

К этому моменту у вас еще нет ни малейшего представления, как построить эту НЕТ-машину, но по меньшей мере вы знаете, что она предположительно должна делать. Поскольку же вы вовсе не обязаны «создать эту чертову штуку прямо сейчас», то мы можем рассмотреть и другие операции.

Вспомним логический оператор, который вы определили как «и» (или ∧) и который подразумевает, что оба аргумента должны быть истинными для того, чтобы утверждение в целом являлось истинным. Другими словами, «( p ∧ q )» будет истинным только в том случае, если истинны и p , и q , и ложным в любой другой ситуации.

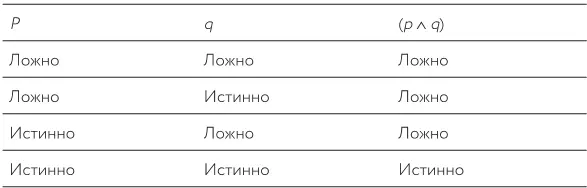
Вот таблица истинности, которая показывает это наглядным образом (табл. 21).

Таблица 21.Таблица истинности для p ∧ q

И точно так же, как и в случае с «не», необходимо трансформировать «истинно» и «ложно» в единицы и нули, чтобы создать первую в мире И-ячейку, которую мы представим следующим образом (табл. 22, рис. 63).

Таблица 22.Входы и выходы для И-ячейки

Единственная деталь головоломки, которой нам не хватает, – это «или», нечто противоположное «и».

Операция «или» между p и q символизируется так ( p ∨ q ), и «( p ∨ q )» будет истинным в случае, если либо p либо q истинно.

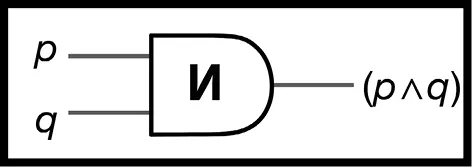
Рис. 63.Представление И-ячейки в графическом виде

Таблица истинности для ИЛИ-ячейки выглядит следующим образом (табл. 23, рис. 64).

Таблица 23.Входы и выходы для ИЛИ-ячейки

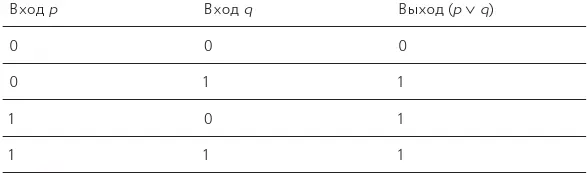
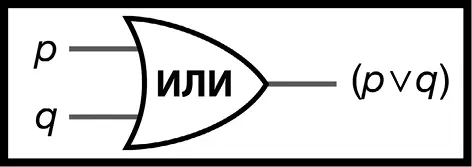
Рис. 64.ИЛИ-ячейка

Три базовые ячейки можно использовать для того, чтобы сконструировать более сложные. Например, поставьте НЕТ-ячейку после И-ячейки, и у вас получится НЕТИ-ячейка, выглядящая следующим образом (табл. 24, рис. 65).

Таблица 24.Входы и выходы для НЕТИ-ячейки

Рис. 65.Полная НЕТИ-ячейка

С целью сохранения времени мы не рисуем НЕТ-ячейку и И-ячейку вместе, мы совмещаем их в одном изображении, вот так (рис. 66).

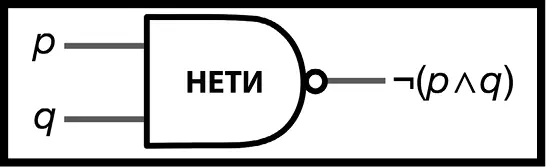
Рис. 66.Упрощенная НЕТИ-ячейка

НЕТИ-ячейка функционирует точно так же, как НЕТИ-ячейка, которую мы нарисовали сначала, но ее можно изобразить быстрее.

И мы можем продолжить, комбинируя разные ячейки, используя НЕТИ-ячейку, ИЛИ-ячейку и И-ячейку, чтобы создать новую ячейку, которая даст на выходе 1, если и только если на одном из входов есть 1. Любой другой вариант, и на выходе будет 0. Подобная ячейка именуется «эксклюзивное или» (ЭИЛИ), и ниже показано, как ее создать (рис. 67, табл. 25).

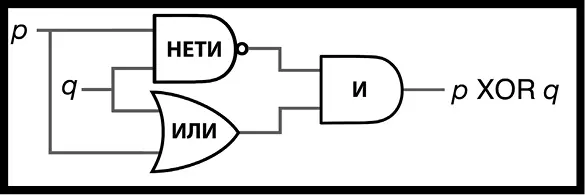
Рис. 67. Полная ЭИЛИ-ячейка

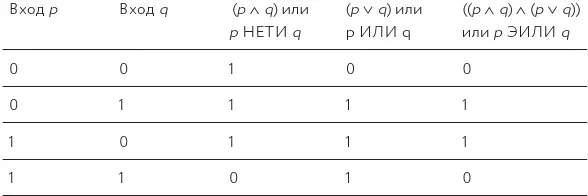
Таблица 25.Таблица истинности, доказывающая, что вы можете получить ЭИЛИ-ячейку из НЕТИ-ячейки, ИЛИ-ячейки и И-ячейки

И точно так же, как и в предыдущем случае, мы дадим этой ячейке собственный символ (рис. 68).

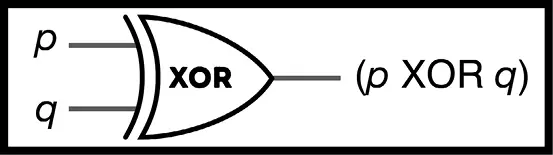
Рис. 68.Упрощенная ЭИЛИ-ячейка

Забавный факт: кроме НЕТИ-ячейки и ЭИЛИ-ячейки, которые вы только что придумали, вы можете на самом деле сконструировать ячейку, дающую любой возможный набор выходных данных, используя только И-ячейку, ИЛИ-ячейку и НЕТ-ячейку, с которых вы начинали [239].

Правильно.

Ну, давайте определим, как должна выглядеть я чейка, способная складывать. Попробуем начать с оснований – с прибавления друг к другу бинарных чисел, что позволит нам создать клево выглядящую таблицу истинности для всех возможных исходов (табл. 26).

Таблица 26.Невероятно, но не первый раз в этой книге мы объясняем, что 1 + 1 = 2

Фишка в том, что бинарная система имеет дело с нулями и единицами, и вы получили бинарное 10 (то есть 2) в одном из вариантов. Так что давайте разобьем наш канал выхода на два, чтобы каждый представлял один бинарный разряд, вот так (табл. 27).

Таблица 27.Как складывать до двух в бинарном отображении

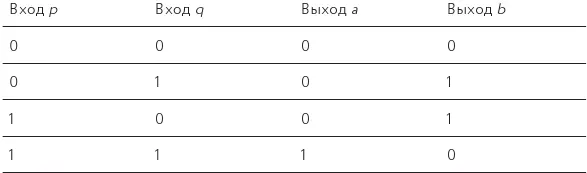
Теперь у нас есть два входа (представляющих два одноразрядных бинарных числа, которые вы хотите сложить) и два выхода (представляющих двухразрядное решение, снова выраженное бинарным образом). Мы поименовали их a и b , и вместе они кодируют то, к чему приводит сложение разрядов на входе.