Альманах «Знак вопроса» - Знак вопроса, 2005 № 02

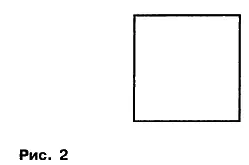
Длиной периметра Р = 8, длиной полу-периметра L = 0,5 Р = 4, площадь поверхности А = 4 и число П = L 2/A = L/r = 4. Визуальный образ квадрата представлен на нижеследующем рисунке 2. Запомним подчеркнутое равенство: (при условии r=1) П = L = A = 4. Данное равенство определяет визуальный образ числа четыре.

5. Число пять представляет собой ромб, у которого диагонали относятся как 1:2, или трапецию у которой периметр Р = 10. У обеих фигур радиус вписанной окружности г = 1, полупериметр L = 0,5 Р = 5, площадь поверхности А = 5. У ромба А = 0,5 (2 √5) (√5) = 5, у трапеции А = 0,5 (1 + 4) 2 = 5. Число П = L 2/A= = L/r = 5. Визуальный образ фигур представлен на рисунках 3 и 4. Запомним подчеркнутое равенство: (при условии г = 1) П = L = А = 5. Данное равенство определяет визуальный образ числа пять.

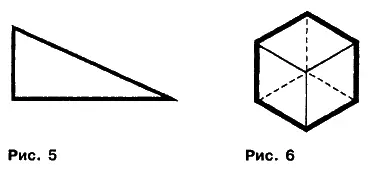
6. Число шесть представляет собой египетский треугольник, с отношением сторон 3: 4: 5, или куб, состоящий из двух «полукубов», разделенных длиной сети — L. Длина сети или полупериметр L = 0,5 Р = 6; площадь поверхности А = 6; число П = 6. В данном случае числовое выражение объемного образа куба определяется по формуле Шварца П = А 3: 36 V 2, где V — объем куба. Визуальный образ фигур представлен на рисунках 5 и 6. Запомним подчеркнутое равенство: (при условии r = 1) II = L = А = 6. Данное равенство определяет визуальный образ числа шесть.

7. Число семь представляет собой замкнутую прямоугольную полосу с отношением сторон 2,5 × 3,0 и вырезанным центром в форме прямоугольника с отношением сторон отверстия 1,0:0,5. Число семь может быть представлено двумя шестиугольниками с отношением сторон 1,25: 1,25: 1,00: 1,25: 1,25: 1,0, откуда Р = 7; L = 3,5; А = 1,5 + 2 = 3,5. Шестиугольник с таким соотношением сторон имеет единичную масштабность контура и плотности сети, т. е. г = A/L = d = L/A = 1. Шестиугольник модулируется четырьмя египетскими треугольниками с площадью А = 0,375 × 4 и двумя квадратами с площадью 1,0 × 2 = = 2,0. Визуальный образ описанных фигур представлен на рисунках 7 и 8. Запомним подчеркнутое равенство (при условии r=1) П = L = A = 7. Данное равенство определяет визуальный образ числа семь.

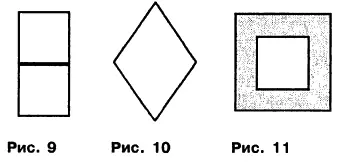
8. Число восемь можно представить визуально состоящим из двух квадратов каждый из которых имеет стороны 2 × 2, вписаны названные квадраты в прямоугольник с отношением сторон 1:2. Число восемь можно представить квадратом 3 × 3, у которого вырезан в центре квадрат со сторонами 1 x 1, точнее это квадратная полоса шириной r = 1 и с нейтральной зоной в центре. Кроме того, число восемь может быть представлено ромбом, у которого два угла острые и определяются величиной 30° = π l/6, и два утла тупые с величиной 150° = 5 π/6. Все названные фигуры изображены на рисунках 9, 10, 11. Они имеют единичную масштабность и плотность сети. Запомним подчеркнутое равенство (при условии r = 1) П = L = А = 8. Данное равенство определяет визуальный образ числа восемь.

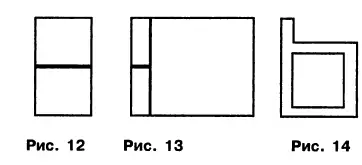
9. Число девять визуально представляется двумя прямоугольниками с отношением сторон 1:2, вписанными в квадрат со сторонами 3 x 3. Такую фигуру можно отобразить тремя прямоугольниками с отношением сторон 1: 2 каждый, и вписанными в прямоугольник со сторонами 2 × 4,5. Кроме того, число девять изображается буквой «мягкий знак» с шириной полосы r = 1. Все описанные фигуры имеют следующие параметры: П = L = А = 9 при масштабности r = 1 и плотности сети d = 1, т. е. r = A/L = d = L/A = 1. Описанные фигуры видны на рисунках 12, 13, 14. Запомним подчеркнутое равенство (при условии r=l) П = L = A = 9. Данное равенство определяет визуальный образ числа девять.

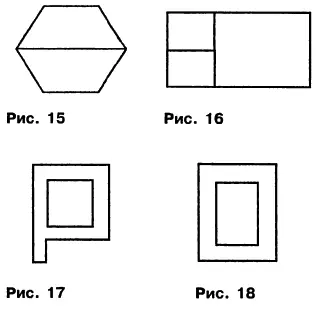
10. Число десять изображено как две трапеции, вписанные в шестиугольник со сторонами 2,5; 1,0; 2,5; 2,5; 1,0; 2,5. Две трапеции, вписанные в шестиугольник, могут отображаться двумя квадратами со сторонами 1,0 × 1,0 и одним прямоугольником со сторонами 2,0 × 4,0. Названные элементы структуры вписаны в прямоугольник со сторонами 2,0 × 5,0. Кроме того, число десять изображается буквами «Р» и «О». Все названные фигуры имеют следующие параметры: П = L = А = 10 при масштабности контура r = 1 и плотности сети d = 1, т. е. r = A/L = d = L/A = 1. Описанные фигуры видны на рисунках 15, 16, 17, 18. Запомним подчеркнутое равенство (при условии г = 1) П = L = А= 10. Данное равенство определяет визуальный образ числа десять.

11. Число одиннадцать представляется несколькими структурами, однако на рисунке 19 и 20 даны две конфигурации. Первая структура из одного контура дана в форме буквы «Р», другая структура состоит из пяти контуров, вписанных в прямоугольник со сторонами 5,5 × 2,0. Площадь фигур и полупериметр равны числу П = 11 при масштабности структуры r = 1 и плотности сети d = 1, т. е. r = = A/L = d = L/A = 1. Описанные фигуры представлены на следующих рисунках:

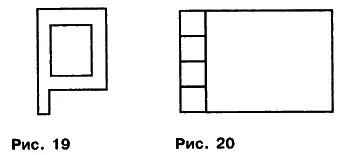
На рисунке 19 изображен один контур (N = 1), а на рисунке 20 изображены пять контуров (N = 5). Структуры с промежуточным числом контуров, т. е. N = 2; 3, 4 предлагается читателям определить самостоятельно и направить в банк объемно-планировочных структур и брэндов. Если структуры и брэнды получают высокую качественную и эстетическую оценку, то они будут занесены в банк под именем или псевдонимом автора. Брэнд (от английского слова brand) находит в наше время очень широкое применение и включает такие понятия, как марка; символ; эмблема; клеймо; тавро; лайб; этикетка; ярлык. Закрепление брэнда в форме визуального и вербального символа укрепляет авторское право разработчика брэнда и его владельца. Запомним подчеркнутое равенство (при условии r=l): П = L = А = 11. Данное равенство определяет визуальный образ числа одиннадцать.

12. Число двенадцать рассмотрим в качестве последнего примера «отображения». Это объясняется тем, что оно (число 12) может быть представлено структурами из одного, двух, трех и четырех контуров, которые изображены на рисунках 21, 22, 23, 24, 25, 26.

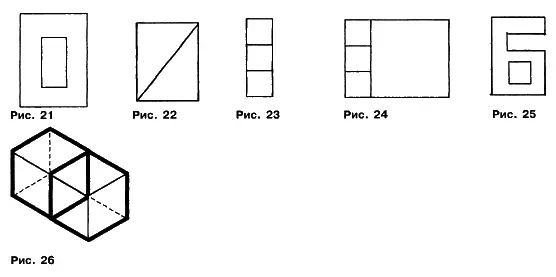
У всех структур периметр Р = 24, площадь, полупериметр, числовое выражение формы равны числу двенадцать, т. е. П = L = А = 12. Представленные рисунки иллюстрируют сам факт произведенного отображения. Так, например, одноконтурная структура на рисунках 21 и 25 отображается в структуру из двух египетских треугольников, такое отображение называется триангуляцией. Далее на рисунке 23 представлены три квадратных контура, которые можно назвать ортогональной структурой. Все структуры, изображенные на рисунках 22, 23, 26, меняют свою форму, при отображении, но не меняют масштабности и плотности. На рисунке 24, хотя общая масштабность и плотность равны единице, но у малого квадрата г = 0,5; d = 2. Большой квадрат имеет r=0,5; d = 2/3 = 0,6 (6). Иными словами, отображение на рисунке 24 происходит не изменением форм контуров, как это было на других рисунках, а изменением плотности и масштабности части структуры и ее целого при сохранении квадратной формы элементов структуры. Рисунок 24 иллюстрирует предмет «новой арифметики», которая изучает соотношение части (три малых квадрата) и целого (один большой квадрат). Традиционная же арифметика изучает соотношение малого и большого. В первом случае, изучая часть и целое, мы имеем дело преимущественно с качественным анализом. В традиционной же арифметике мы имеем дело чаще с количественными преобразованиями.