Альманах «Знак вопроса» - Знак вопроса, 2003 № 04

11_ГРАНЬ_25. В книге Анатолия Виноградова «Осуждение Паганини», написанной в 1936 году (Госиздат «Художественная литература», М., 1953 г., всего 351 страница), на странице 322 один из персонажей романа произносит следующую фразу: «Я думаю, что достаточно десяти концертов, чтобы на одиннадцатом Паганини выронил скрипку и умер». Как известно, в конце жизни великий скрипач и композитор сильно болел и состояние его здоровья «знатоки» оценили по 11-балльной системе.

11_ГРАНЬ_26. В газете «Завтра» (№ 43/2002, октябрь, страница 6) в статье-интервью Владимира Рыбакова с заместителем генерального конструктора РКК «Энергия» имени С. П. Королева Николаем Зеленщиковым, возможно, впервые обнародован тот факт, что 11 процентов акций знаменитого на весь мир предприятия оказались в руках компании «Оппенгеймер» из США. Из других доверительных источников стало известно, что представитель этой компании Сидорович введен в состав директоров РКК «Энергия» имени С. П. Королева.

11_ГРАНЬ_27. Испытания первой в мире радиолокационной системы (ведущий конструктор — Ощепков Павел Кондратьевич) состоялись 11 июля 1934 года в Ленинграде. Обратитесь, например, к книге Льва Викторовича Жигарева «Следы в эфире», страница 127 (издательство «Знание», Москва, 1965 г.).

11_ГРАНЬ_28. Необходимо привести примеры малозначительных или ложных фактов, касающихся числа 11. Им не место в музее, в лучшем случае — лежать им долго в запаснике. Это контрпримеры, подобные которым просим нам не присылать. Вот понадобилось мне сменить книжечку платежных бланков при оплате за газ. И комната, в которой их выдают, оказалась с номером 11 на втором этаже здания, что стоит недалеко от городского рынка. Другой не лучший пример. Книга Карела Чапека «Рассказы из одного кармана», страница 80 (издательство «ЛИДОВЕ НАКЛАДАТЕЛСТВИ», Прага, 1981 г.). Герой рассказа «Поэт» сообщает номер авто-мобиля-нарушителя стихами:

Здесь зашифрован номер авто 235. Меня подвела память, подумал, что палочки — это число одиннадцать. Когда же заглянул в книгу с рассказом, выяснилось, что «барабан» — это нижняя часть цифры 5, а под «палочками» подразумеваются два штриха над нижним полукружьем пятерки, к разочарованию моему — совсем не 11. Число 111 не делится на 11 и тоже являет пример ложного пути. Быть католиком в Англии всегда требовало и требует определенного мужества, а Толкиен был католиком, что никак не связано с его 111-летием. Это странное число все же неожиданно вливается в тематическую направленность нашей публикации через адрес Мемориального музея космонавтики в Москве: улица Мира, 111.

11_ГРАНЬ_29. 11 декабря 1790 года от Рождества Христова, как говорят теперь, — по старому стилю, русские войска под командованием Александра Васильевича Суворова взяли Измаил, о чем можно прочитать на странице 293 в книге О. Н. Михайлова «Суворов» (издательство «Янтарный сказ», Калининград, 1995 г.).

11_ГРАНЬ__30. И все же 11 — единственное симметричное простое число с четным количеством цифр в десятичной записи. См. ГРАНЬ 11-3. Доказательно покажем это. Например, так:

АББА = А × 1000 + Б × 100 + Б × 10 + А = А × 1001+Б × 110 = А × 7 × 11 × 13 + Б х 11 × 10 = 11 × (91А+10Б).

Число вида 111 111 называется репьюнитой, от английского «повторяющаяся единица». Любая репьюнита с четным количеством разрядов делится на 11. Вы это легко можете проверить самостоятельно. Назовем цифровой тонкостенной трубою, или просто трубою, десятичное число, начинающееся и заканчивающееся единицей и имеющее только нули в середине. Четная, по числу разрядов, труба всегда делится на 11, так как

100 001 = 99… 90 + 11 = 90 × (111 111) + 11 = 11 x [90 × К+1],

где количество девяток — четное, репьюнита в круглых скобках — тоже с чет-ным числом единиц, К — некоторое целое число. А любое симметричное число с четным количеством разрядов вида АБ… БА представляет собой систему вложенных друг в друга труб с поправкой для каждой на некоторый арифметический множитель (степень десяти, умноженная на одноразрядную цифру). Разобрав конструкцию АБ БА на трубы-слагаемые (со «стержнем» 11 в середине, домноженным на одноразрядное целое число), легко видеть, что каждое слагаемое делится на 11, а значит, и каждое число подобного вида тоже делится на 11.

Эта «задачка» была предложена вниманию школьников трех восьмых классов одного из ведущих учебных заведений города. Ответа они сразу не получили, а потом о проблеме забыли. Оказалось, что детям нужно помогать. Это я и делаю настоящей «гранью».

118_ГРАНЬ_8. Приложим «масштабные линейки» к числу 118:

• Фибоначчи: 89(11), 118, 144(12);

• простые: 113(30), 118, 127(31);

• квадраты: 100(10), 118, 121(11);

• кубы: 64(8), 118, 125(5).

118_ГРАНЬ_9- В газете «Советская Россия» № 121 от 24.10.2002 за четверг на 5-й странице заметка В. К. Шевченко «Чаща на пашне» с подзаголовком «На курском направлении» начинается так: «На 118-м километре от Москвы по Курской дороге есть у меня «имение» — пресловутые шесть соток…»

137_ГРАНЬ_1. За 15 лет существования долговременной орбитальной космической станции «Мир» на ее борту побывало 137 космонавтов.

137_ГРАНЬ_2. Десятый простома-гичный квадрат третьего порядка имеет в центре (главный параметр!) простое число 137.

Такой отдел в МЧИС открыт впервые. Пока дадим только часть его экспозиции и покажем магические квадраты третьего порядка, иначе называемые простомагичными, поскольку они заполнены лишь различными простыми числами. Эти квадраты упорядочены по нарастанию центральных чисел и пронумерованы.

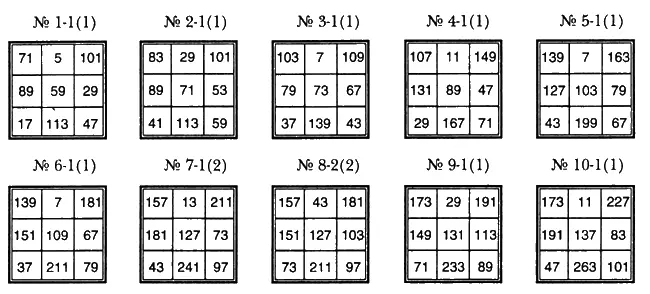
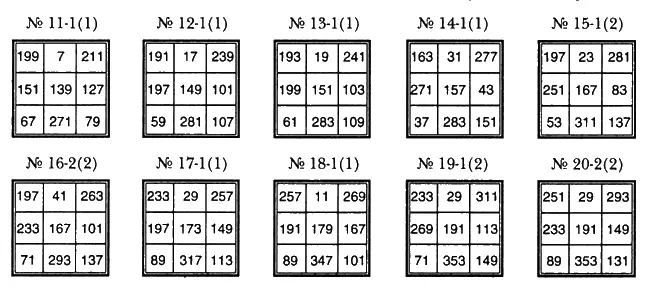
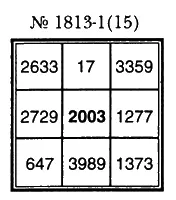
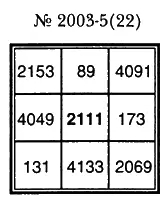
Число в скобках при номере квадрата указывает на длину серии, если сказать иначе — на количество квадратов с «одинаковым центром». Число, стоящее слева от скобок, сообщает о внутреннем порядковом номере квадрата в серии. Серии длины два на множестве публикуемых 20 квадратов обнаруживаются у номеров квадратов 7 и 8 при центральном простом параметре 127, у номеров квадратов 15 и 16 при центральном простом параметре 167 и у номеров квадратов 19 и 20 при центральном простом параметре 191. Просматривая этот начальный фрагмент бесконечного перечня простомагичников, можем отметить такой факт: у простых центральных чисел 2, 3, 5, 7,11,13,17,19, 23, 29, 31, 37,41,43,47 и 53 простомагичных квадратов «нет в природе». Нельзя построить их и для простых центральных чисел 61, 67, 79, 83, 97,101,107,113, 163 и 181. Все 20 девятиклеточников, с 1 по 20, как единый ранжированный и пронумерованный ряд, были впервые опубликованы в совпадающих номерах ежеконцертника «Звоны», начиная с 11 декабря 1996 года по 28 февраля 1998 года включительно.