Сергей Парновский - Как работает Вселенная: Введение в современную космологию

Книга Стивена Вайнберга (1981) является популярным изложением стандартной космологической модели Джорджа Гамова. Она легко читается, в ней нет уравнений, а ее содержание, несмотря на множество открытий, сделанных с 1977 г., когда она была написана, в основном все еще актуально, потому что космологическая постоянная не играет существенной роли в ранней Вселенной.

Помимо книг мы также включили некоторые электронные препринты обзорных статей на английском с сайта arXiv.org. Их тематика должна быть довольно ясной из их названия. Приводим их как arXiv:{что-то}, и вы можете скачать их в интернете, набрав в вашем браузере www.arxiv.org/abs/{что-то}, где {что-то} – это то, что находится в ссылке после двоеточия и до квадратных скобок. Или вы можете просто поискать их на просторах интернета – это тоже отлично работает. Обратите внимание, что большинство из ссылок на arXiv (но не все) – научные статьи, ориентированные на профессиональных ученых.

В дополнение к этому мы настоятельно рекомендуем посетить веб-сайт по космологии Неда Райта, доступный по адресу http://www.astro.ucla.edu/~wright/cosmolog.htm (с русским переводом на http://cosmologiya.narod.ru/cosmolog.htm), который содержит много полезной информации и регулярно обновляется.

В этом приложении мы описываем ΛCDM-модель, используя нерелятивистскую космологию. Это приложение гораздо больше похоже на учебник, чем на научно-популярную литературу. Хотя оно довольно простое, в нем содержится много математики, что и явилось причиной, по которой мы отделили его от остальной части книги.

Строго говоря, здесь мы вышли за пределы применимости нерелятивистской космологии. Тем не менее мы продолжаем использовать нерелятивистское приближение для более общего случая эволюции Вселенной, заполненной различными видами материи. Для этого мы должны применить один результат ОТО, о котором писали в разделе 1.3.

Для вещества с ненулевым давлением в законе тяготения Ньютона вместо полной массы ρV мы должны использовать величину (ρ + 3p/c2)V = (ε + 3p)V/c2. Здесь р – давление, ρ – плотность массы, ε – плотность энергии, а V представляет собой объем сферы, заполненной материей. Эта замена получается как ньютоновской предел ОТО. Соотношение ε = ρc2 является следствием хорошо известной формулы E = mc2. После того как мы применим этот трюк, все формулы нерелятивистской космологии в точности совпадут с уравнениями релятивистской.

Теперь мы имеем возможность ввести нерелятивистский аналог космологической постоянной. Это странный вид материи с плотностью и давлением, определяемыми формулой (2.35), и с уравнением состояния p = –ε. Из уравнения (2.31) мы видим, что обе плотности – вещества и энергии – положительны, давление отрицательно и ни одна из этих величин не меняется по мере расширения Вселенной.

Рассмотрим решение де Ситтера в рамках нерелятивистской космологии. Еще раз рассмотрим пробную частицу, находящуюся на сферической поверхности с радиусом r, и поместим условный центр Вселенной в центр этой сферы. На этот раз сфера заполнена веществом, имитирующим космологическую постоянную с уравнением состояния pΛ = –c2ρΛ = –εΛ. Ускорение этой пробной частицы

Мы учли, что множитель (ε + 3p) для такой материи с p = –ε равен –2ε. Это соответствует расширению с постоянной Хаббла, равной

Параметр замедления (2.23) в этом случае равен –1, так что мы имеем дело с ускоренным расширением Вселенной. Это не удивительно, так как правая часть уравнения (A.1) всегда положительна, что означает гравитационное отталкивание, или антигравитацию.

В случае пылевидной материи существует три возможных космологических сценария (три решения Фридмана). В нашем случае есть один сценарий (решение де Ситтера). Вспоминая аналогию с мячом, который пнули вверх, мы можем предположить, что шар, гравитационно отталкиваясь от планеты, приобретает все увеличивающуюся скорость и не имеет другого выбора, кроме как улететь за ее пределы бесконечно далеко.

Метрика де Ситтера интересна со многих точек зрения и активно используется в космологии, но она не описывает реальную Вселенную. Причина заключается в том, что наша Вселенная содержит не только космологическую постоянную или темную энергию, но еще и много материи, которая играет важную роль в космологии. Большая ее часть существует в виде небарионной темной материи. Мы также знаем, что эта темная материя движется значительно медленнее скорости света. Такая форма темной материи называется холодной темной материей. Ее давление незначительно по сравнению с плотностью энергии, и она похожа на пылевидную материю, которую мы рассматривали ранее.

Модель, которая включает в себя как космологическую постоянную – Λ, так и холодную темную материю – CDM, метко прозвали ΛCDM-моделью. Естественно, большая часть обычной барионной материи также холодная и может рассматриваться вместе с холодной темной материей. Мы просто заменим и то и то на пылевидную материю, пока речь идет только о параметрах эволюции Вселенной. При рассмотрении, скажем, барионных акустических колебаний эти виды материи существенно различаются.

Таким образом, мы рассматриваем сферу, заполненную двумя видами материи. Первый из них соответствует пылевидной материи с энергией и плотностью массы εm = c2ρm. Здесь индекс m относится к материи как темной, так и барионной. Ее давление практически отсутствует: pm ≈ 0. Материя с уравнением состояния pΛ = –c2ρΛ = –εΛ заменяет космологическую постоянную и обозначается индексом Λ. Как видно из уравнения (2.31), значения этих величин постоянны. В частности, ρΛ = const. Разделив ρm и ρΛ на критическую плотность (2.11), мы получаем параметры их плотности Ωm и ΩΛ соответственно. Они равны

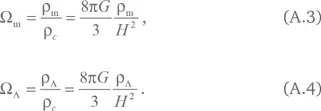
Все три модели Фридмана соответствуют ΩΛ = 0. Случаи замкнутой, плоской и открытой моделей соответствуют Ωm > 1, Ωm = 1 и Ωm < 1. Модель де Ситтера соответствует Ωm = 0, ΩΛ = 1.

Параметры плотности и Ωm и ΩΛ изменяются с течением времени, потому что постоянная Хаббла зависит от времени, как и плотность вещества (2.8). Значение ρΛ остается постоянным.