Виталий Бронштэн - Серебристые облака и их наблюдение

3) Положение линии горизонта на снимке.

4) Географические координаты наблюдательного пункта.

Рассмотрим простой способ определения координат центра снимка. Для его обозначения на снимке проводим простым карандашом по эмульсии негатива близ его центра отрезки диагоналей, пересечение которых и обозначит центр снимка. Для удобства делаем в этом месте легкий накол иголкой.

Для определения координат этого центра, азимута A 0и высоты h 0, необходимо иметь на снимке несколько точек с известными координатами A, h . Это могут быть городские сооружения (вершина шпиля башни, заводской трубы и т. д.) или специально установленные столбы с лампочками наверху, о которых уже говорилось. Не рекомендуется выбирать в качестве ориентиров верхушки деревьев или тонкие приемные телеантенны, так как они могут раскачиваться ветром. Координаты выбранных ориентиров определяются с помощью теодолита.

В качестве опорных точек можно использовать и звезды, для которых по известному моменту съемки и экваториальным координатам вычисляются горизонтальные координаты А, h. Как это делать, рассказано в Постоянной части «Астрономического календаря» и в учебниках общей астрономии для вузов. В значения высоты звезд вводятся поправки за рефракцию.

Если аппарат имеет наклон оптической оси к плоскости горизонта на угол α ( α ~= 10°), то целесообразно ввести вспомогательную систему сферических координат, наклоненную на угол α к горизонтальной системе (рис. 40).

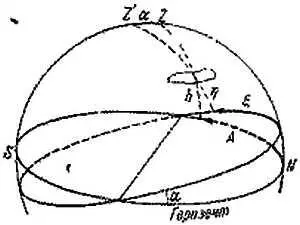
Рис. 40. Вспомогательная система сферических координат ζ, η.

Роль «азимута» будет играть угол ζ роль «высоты» — угол η . На снимке мы с помощью прямоугольной прозрачной палетки или измерительного прибора измеряем прямоугольные координаты деталей х, y отсчитываемые от найденного нами центра снимка. Если координаты приходится отсчитывать от другого начала (обозначим их х ', у '), то нужные нам координаты х, у мы найдем по формулам

x = х' + х c, у= у' — у c, (23)

где x c, у с— координаты центра снимка в той же системе.

Далее по значениям х, y находим сферические координаты ζ, η по формулам

tg ζ= x/ F, (24)

tg η= ( y/ F)∙(cos ζ), (25)

При этом мы полагаем, что координаты центра снимка ζ 0— 0, η 0= 0, и учитываем знаки каждой координаты, считая их положительными вверх и вправо от центра. Найдя для каждого ориентира значения ζ, η , вычисляем разности А — А 0по формуле

sin ( А— А 0) = (cos η∙sin ζ)/cos h, (26)

Значения A, h нам известны из прямых измерений теодолитом (а для звезд из вычислений). Точки, для которых А — А 0 > 10° и h — h 0> 10°, отбрасываем, для остальных по А — А 0и известным А находим A 0и из полученных значений (которые должны слабо отличаться друг от друга) находим среднее. Это и будет азимут центра снимка. Его высота h 0находится по формуле

h 0 = ( h— η)/cos ( A— A 0), (27)

Значения h 0, полученные по разным ориентирам, тоже усредняем. Отдельные значения h 0должны отличаться друг от друга не более чем на 2–3'. Если получатся более сильные расхождения, значит, допущены ошибки в измерениях или вычислениях, и их надо проверить.

До сих пор мы предполагали, что изображение линии горизонта на снимке параллельно нижней стороне кадра. Однако если мы применяем три аппарата для панорамной съемки, как показано на рис. 37, для двух крайних аппаратов это условие выполнено не будет. Поэтому приведем формулы, с помощью которых можно построить изображение линии горизонта в этом случае.

Уравнение этой линии в прямоугольных координатах имеет вид [7] См. книгу: Бугославская Е. Я. Фотографическая астрометрия. М.: Гостехиздат, 1947, с. 101. )

Поскольку Нам известно h 0и для каждого ориентира его высота h , мы можем решить квадратное уравнение (28) относительно у ( х берем из измерении) для каждого ориентира.

Откладывая затем отрезки, равные у , вниз от точки ориентира, получим ряд точек горизонта, которые должны лечь на дугу малой кривизны, близкую к прямой линии.

Однако полученная линия горизонта — лишь первое приближение, поскольку координаты х , использованные нами в уравнении (28), измерены в системе, слегка повернутой относительно проекции линии горизонта. Выйти из положения можно двумя способами. Во-первых, можно заново измерить значения х, у , сориентировав ось х палетки или измерительного прибора параллельно найденной в первом приближении линии горизонта, и затем повторить расчет по формуле (28). Мы получим новую линию горизонта, которая должна пройти близко от первой или даже может совпасть с ней.

Второй способ состоит в том, что измеряется угол поворота γ найденной в первом приближении линии горизонта относительно оси, проходящей параллельно нижней стороне кадра. Новые координаты х, у выразятся тогда через старые х ', у ' формулами

x= x'∙cos γ+ y'∙sin γ,

y= — x'∙sin γ+ y'∙cos γ, (29)

причем угол γ считается положительным, если поворот осей координат происходит против часовой стрелки, и отрицательным, если по часовой стрелке. После этого по значениям х, у вновь находим линию горизонта.

Оба способа целесообразно применять параллельно, для взаимного контроля. Подчеркиваем, что все эти расчеты, измерения и построения нужно делать не для каждого кадра, а лишь один раз для данной ориентации аппарата. Поэтому целесообразно заранее позаботиться о фиксации положения как аппаратов на установочной доске, так и самой доски на столбе (столе). Этим мы намного облегчим себе работу по обработке фотографий.

Необходимо еще раз подчеркнуть необходимости производить математическую обработку фотографий серебристых облаков, без которой они превратятся в красивые, но почти бесполезные картинки. Не надо бояться вычислений. Напротив, надо научиться быстро и правильно вычислять и, что не менее важно, правильно и аккуратно записывать результаты вычислений. Ни в коем случае нельзя вычислять на клочках бумаги, а тем более — выбрасывать потом эти листки. Все вычисления надо вести в специальной тетради, причем записываются не только окончательные, но и все промежуточные результаты вычислений. Формулы, по которым ведутся вычисления, выписываются сверху, после чего все обозначения, к числа располагаются столбиками. Арифметические знаки действий (плюс, минус и др.), а также знак равенства не пишутся. Перед отрицательными величинами ставится знак минус. Приведем пример расположения вычислений (табл. 2).