Виталий Бронштэн - Серебристые облака и их наблюдение

Введем прямоугольную геоцентрическую систему координат с началом в центре Земли. Ось X направим к точке пересечения экватора с начальным (гринвичским) меридианом, ось Y — к точке экватора с восточной долготой 90°, ось Z — к северному полюсу Земли.

Далее введем две топоцентрическне системы координат с началом в каждом из двух пунктов наблюдений. Оси расположим параллельно осям основной геоцентрической системы.

Определенные путем измерения на фотографиях горизонтальные координаты точки облака h, А переводим в экваториальные координаты t, δ по известным формулам

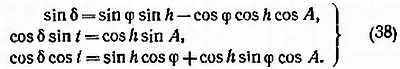
В формулах (38) φ — широта пункта наблюдения, δ — склонение, t — часовой угол данной точки облака. Далее для сокращения записи там, где формулы одинаковы для обоих пунктов, мы будем писать индекс i ( i = 1, 2). Топоцентрические координаты точки С облака будут равны

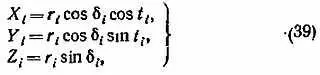
где r i— расстояния до точки С от обоих наблюдательных пунктов по прямой (по лучу зрения). Введем обозначения (для краткости)

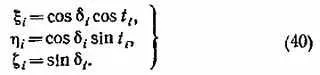
Тогда получим следующую систему из шести уравнений пятью неизвестными — геоцентрическими координатами точки С ( Х с, Y c, Z c) и расстояниями r 1, r 2:

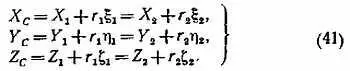
Эту систему можно решить методом наименьших квадратов, изложенным в Постоянной части «Астрономического календаря» (7-е изд. — М.: Наука, 1981, с. 521–532). Для тех, кто не знаком с этим методом, можно рекомендовать следующий порядок вычислений.

Отвлечемся на время от левых равенств в системе (41) и от величин Х с, Y c, Z c. Тогда у нас останутся три условных уравнения с двумя неизвестными r 1, r 2. Их решение по методу наименьших квадратов дает

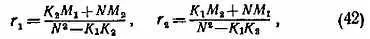
где введены обозначения

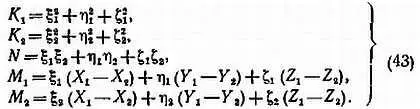
Подставляя r 1, r 2в уравнения (41), получим значения Х с, Y c, Z c. Из двух значений каждой из этих величин (по i = 1 и i = 2) берем среднее. Затем находим радиус-вектор точки С относительно центра Земли р с,

p c = √( Х 2 с+ Y 2 c+ Z 2 c), (44)

и наконец, высоту точки С серебристого облака

H= p c— R, (45)

где R — радиус Земли на широте проекции серебристого облака, которую можно найти по формуле

φ' = arcsin ( Z c/ p c); (46)

аналогично долгота проекции точки С равна

λ= arctg ( Y x/ X c). (47)

Значения R для данной широты φ приведены в Приложении 4 . Там же даны поправки для перевода геоцентрической широты φ ' (получаемой из формулы (46)) в географическую широту φ . В среднем для зоны появлений серебристых облаков φ — φ ' = 10'.

Таким образом, определение высот серебристых облаков методом Дирикиса-Францмана — операция несложная, но требует выполнения многих измерений и вычислений. Лучше всего эти расчеты производить на ЭВМ. Те кружки или группы наблюдателей серебристых облаков, которые имеют такую возможность (используя ЭВМ астрономических или иных научных учреждений, шефствующих предприятий и т. д.), должны составить программу и заложить в нее результаты измерений по всем фотографиям, полученным с двух пунктов. Формулы элементарны, и поэтому любая ЭВМ выдаст результаты за очень короткий срок.

Тем, кто не имеет такой возможности, придется считать на микрокалькуляторах или с помощью таблиц, что тоже не представляет принципиальных трудностей. Придется, правда, потрудиться, но зато наблюдатели и вычислители будут вознаграждены интересными и ценными результатами, которые они получат.

Исследование оптических свойств серебристых облаков удобнее всего проводить методами фотографической фотометрии и колориметрии. Колориметрия — это та же фотометрия, но проводимая через светофильтры. Наконец, по фотографиям, снятым через поляроиды, можно проводить поляриметрию. Методика получения и обработки фотографий во всех трех методах одна и та же, поэтому мы будем описывать их параллельно.

Для того чтобы фотографии серебристых облаков были пригодны для фотометрической обработки, они должны быть высокого качества, хорошо проявлены, отфиксированы и промыты. Но этих требований недостаточно. Фотографии, предназначенные для фотометрии, должны быть калиброваны и стандартизованы.

Калибровка фотографий. Чтобы по почернению негатива определить отношение, яркостей объекта в различных точках (или разных объектов), нужно получить соотношение между почернением и освещенностью. Почернение измеряется с помощью микрофотометра по поглощению луча, проходящего в приборе сквозь изображение на негативе и регистрируемого отсчетами на шкале микрофотометра.

Если мы произведем засветки на фотопластинке или плёнке при измерении освещенности в геометрической прогрессии, а затем измерим оптические плотности на микрофотометре, то мы сможем построить характеристическую кривую фотоэмульсии, выражающую соотношение между освещенностью Е и оптической плотностью почернения D (рис. 45).

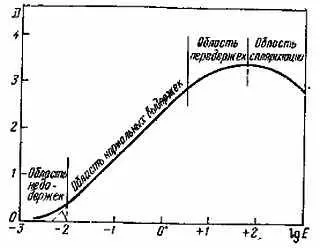
Рис. 45. Характеристическая кривая фотопластинки.

Характеристическая кривая состоит из нескольких участков. Начальный участок, где кривая идет полого, называется участком или областью недодержек . Следующий участок, где кривая близка к прямой, — это область нормальных выдержек (времени экспозиции). Наконец, верхний участок, где наклон кривой снова уменьшается, — область передержек.

При фотометрии серебристых облаков нужно стремиться к тому, чтобы изображения облаков оказались в области нормальной экспозиции. С другой стороны, при фотографической фотометрии необходимо все снимки делать с одинаковым временем экспозиции. Поэтому, учитывая многолетний опыт наблюдателей, будем делать все снимки (включая калибровочные и стандартизационные) с временем экспозиции 30 секунд. Чувствительность пленок должна быть 90—130 единиц ГОСТ.