Иван Ефишов - Таинственные страницы. Занимательная криптография

Единица в Древней Индии могла обозначаться также словами «начало», «тело», «предок», «Вишну», «Брахма».

«Глаза», «близнецы» и «губы» суть парные слова, и согласно правилам они используются для обозначения двойки.

Какому же числу или цифре соответствуют слова «время», «миры» и «Шива»? Те, кто знаком с индуизмом, могут вспомнить, что у Шивы на лбу имеется третий глаз. Тогда становятся понятными аналогии и со временем (у индусов, как и у нас, время делится на прошлое, настоящее, будущее) и с мирами (подземный, наш и небесный).

Таким образом, загаданное число имеет вид *123. Что же находится в первой позиции? Небо, пустой, отверстие. «Пустой» – можно предположить, что это слово подходит, как никакое иное, для обозначения нуля; вспомним, что и латинское nullus означает «никакой». «Отверстие» тоже подходит для обозначения нуля. Небеса также пусты, незримы, как воздух.

Итак, возможный ответ – 0123 или 123. Но зачем записывать 123 так сложно, с нулем впереди? Тем более что нуль появился позднее других цифр; вряд ли после его появления могла сложиться традиция записывать его перед «старыми» цифрами, да и не нужен он там! Правильный ответ в данном случае – 3210: числа в хронограммах, как правило, записывали справа налево.

Американский писатель Дэн Браун (р. 1964) в своем «Коде да Винчи» использовал для декодирования информации числа Фибоначчи. Кратко напомним канву событий, связанных с этими загадочными числами.

В здании Лувра обнаружен труп куратора музея Жака Соньера. Убитый обнажен и лежит в позе, воспроизводящей знаменитый рисунок Леонардо да Винчи «Витрувианский человек». На теле – зашифрованная кровавая надпись: Соньер в последние минуты жизни «использовал собственную кровь в качестве чернил или краски, а собственный обнаженный живот – как полотно». Надпись была следующей:

13-3-2-21-1-1-8-5

На вид идола родич!

О мина зла!

Что за мина зла? Да еще родич какого-то идола… Что касается чисел – если их расположить по возрастанию (1, 1, 2, 3, 5, 8, 13, 21), то мы получим первые восемь чисел бесконечного ряда Фибоначчи. Впрочем, передадим теперь слово главному герою романа, профессору Гарвардского университета Роберту Лэнгдону: «Искаженный ряд Фибоначчи – это ключ. Числа являются намеком на то, как следует расшифровывать остальную часть послания. Соньер специально нарушил последовательность, намекая на то, что такой же подход можно применить и к тексту».

Таким образом, Жак Соньер оставил намек, что написанное им – криптограмма! То есть, переставив буквы в послании, мы получим другой смысл записки. Первая строка записки с искажениями (ведь ряд Фибоначчи тоже искажен) дает «Лиодардо да Винчи!», вторая декодируется как «Мона Лиза!». Смысл записки теперь более или менее ясен: она оставлена куратором Лувра, где и хранится знаменитая картина:

«Леонардо да Винчи! Мона Лиза!»

Указание на знаменитую картину позволило найти золотой ключ к сейфу швейцарского депозитарного банка. Кроме того, числа Фибоначчи оказались также и кодом доступа к этому сейфу.

Но почему Жак Соньер выбрал для кода доступа именно числа Фибоначчи? Вот как это объясняет сам Дэн Браун на страницах романа: «Если превратить последовательность Фибоначчи в простой набор из десяти цифр, она становится практически неузнаваемой. Запомнить легко, а на первый взгляд цифры кажутся выбранными наугад. Гениальный, потрясающий цифровой код, который Соньер никогда бы не забыл».

Рассмотрим историю этого «гениального, потрясающего цифрового кода». Откуда взялись эти цифры?

Совпадение! Их открыл тоже Леонардо, и тоже итальянец, но, увы, не знаменитый да Винчи, а некий купец Леонардо Фибоначчи (1170–1250). В своем первом математическом труде «Книга Абаки» (Liber Abaci, 1202 год) он рассмотрел задачу о размножении кроликов. В результате появились замечательные числа, позже названные именем Фибоначчи:

f 1 = 1, f 2 = 1, f 3 = 2, f 4 = 3, f 5 = 5, f 6 = 8…., f 12 = 144….

Первые два числа в этой последовательности заданы и равны единице, то есть f 1 = 1, f 2 = 1, а каждое последующее число равно сумме двух предыдущих чисел. Например, f 6 = f 5+ f 4(или 8 = 5 + 3). Счет можно продолжить. Так, например, двенадцатое число Фибоначчи равно f 12 = 144.

Числами Фибоначчи можно описать как корзинку подсолнуха, так и расположение спиральных рукавов Галактики.

Отметим, что в своем труде Леонардо Фибоначчи, который по делам торговли не раз оказывался в арабском Алжире, рассмотрел впервые в европейской математике арабскую систему счисления. Привычная нам десятичная позиционная система, которую все мы изучаем в школе, в свое время стала крупнейшим прорывом в математике. Не будь ее, нам пришлось бы до сих пор пользоваться римской нотацией, столь неудобной при вычислениях.

Плавно перейдем к другой задаче по кодированию и передаче информации, где также возникают вездесущие числа Фибоначчи. Но предварим ее небольшим двойным линейным кроссвордом.

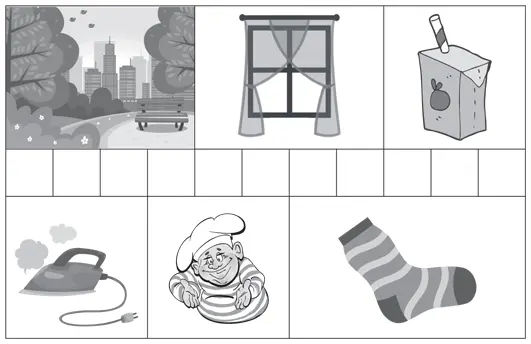
По верхнему ряду рисунков кроссворд разгадывается следующим образом: «парк, окно, сок», по нижнему ряду – «пар, кок, носок».

Как видим, сообщение «паркокносок» можно прочесть двумя способами. В данном случае информацию, состоящую из одиннадцати букв, вы легко дешифровали, используя подсказки-картинки. Но у криптоаналитика подсказок, как правило, нет.

Рассмотрим аналогичную задачу {9}, связанную с передачей информации, также состоящей из одиннадцати символов, но не сопровождающейся дополнительными подсказками.

Вот ее условие. Некоторый алфавит состоит из шести букв, которые для передачи по телеграфу кодируются одним или двумя знаками следующим образом:

•, –, • •, –, • –, – •.

При передаче некоего слова не сделали промежутков, отделяющих букву от буквы, так что получилась сплошная цепочка точек и тире, состоящая из одиннадцати знаков.

Сколькими способами можно прочесть переданное слово?

Сделаем задачу более наглядной. Предположим, что вам передали следующее слово:

• • – • – • – •

Попробуйте для начала разобраться с этим частным случаем.

Задача полностью аналогична той, которую вы разгадывали в линейном кроссворде. Но там вы отделяли друг от друга слова, а здесь придется отделить закодированные буквы в слове. Известно, что при передаче телеграмм или радиограмм применяется азбука Морзе, в которой, например, буква А всегда кодируется двумя знаками • –, тогда как буква Е – это одна точка •, а буква Т – просто тире – . Таким образом, получив сообщение из двух знаков • – (в котором преднамеренно пропущен пробел), вы можете его декодировать либо как букву А, либо как две буквы ЕТ.