Сергей Титов - Естествознание. Базовый уровень. 10 класс

1. Что такое граф? Что такое вершины и рёбра графа? Что такое «полный» и «пустой» граф?

2. Какой граф называется организованным?

3. Какие типы взаимодействия между элементами существуют при отрицательной, положительной и антагонистической обратных связях?

4. Что такое метод чёрного ящика?

1. Приведите примеры взаимоотношений организмов в природе, основанных на положительной обратной связи.

2. Приведите примеры систем с отрицательной, положительной и антагонистической обратными связями. Начертите организованные графы, в которых обозначьте типы связей между элементами.

3. Существует группа людей, состоящая из восьми человек. Участники этой группы А, Б и В образуют первую подгруппу, а участники Г, Д и Е – вторую. Члены каждой подгруппы дружат между собой, но не любят членов другой подгруппы. Участники Ж и З находятся во взаимных дружеских отношениях и не вмешиваются в отношения участников этих двух подгрупп. Наконец, в группе имеется участник И, который умудряется дружить со всеми членами коллектива. Нарисуйте граф, иллюстрирующий отношения в группе.

В жизни нам часто приходится сталкиваться с наблюдениями или испытаниями, результаты которых невозможно предвидеть, потому что они зависят от различных обстоятельств, которые мы не знаем или не можем учесть. Часто мы говорим, что некое событие скорее всего произойдёт или, наоборот, что его наступление маловероятно. «Вряд ли завтра будет дождь» или «Скорее всего, мы на следующей неделе поедем на дачу». Что стоит за этими высказываниями и можно ли их выразить в строгой математической форме? Идея о том, что можно как-то измерить значения событий, которые ещё не произошли, но в принципе могут произойти, возникла, как ни странно, в связи с изучением закономерностей выигрышей в азартных играх, таких как карты или кости (рис. 195). Невозможно предсказать, какая карта будет вынута из перетасованной колоды или сколько очков окажется на верхней грани упавшей кости. Однако можно заметить, что если мы будем много раз вытаскивать карты, то туз бубен появится почти точно столько же раз, сколько и тройка треф. Количество выпавших шестёрок на кости будет почти точно такой же, как и количество единиц.

Рис. 195. Изучение закономерностей выигрышей в азартных играх привело к мысли, что можно измерить вероятность ещё не наступившего события

В этих случаях говорят, что все карты колоды или все грани кубика имеют равную вероятность быть вынутыми или выброшенными.

Назовём событие, которое в настоящее время нас интересует, благоприятным. Например, таким событием будет выпадение шестёрки на игральной кости. Если мы будем бросать кость много раз, то увидим, что отношение числа благоприятных событий к общему числу событий, т. е. ко всем результатам бросания кости, будет оставаться постоянным. (В данном случае оно будет равно 1/ 6.) Это отношение называют вероятностью наступления благоприятного события. Для того чтобы правильно определить вероятность, требуется провести очень много испытаний. Если мы бросим кость один раз, то число благоприятных событий может быть только нулём или единицей. Если бросить кость два раза, то очень возможно, что шестёрка не выпадет ни разу, хотя вполне может случиться, что она окажется сверху в обоих случаях. Поэтому вероятностью, строго говоря, надо называть предел отношения благоприятных событий к общему числу событий, когда общее число событий стремится к бесконечности. Ввиду того что число благоприятных событий не может быть меньше нуля и больше числа всех событий, вероятность представляет собой число, которое может принимать значения от 0 до 1. В математике вероятность обычно выражается буквой р, так что 0 ≤ р ≤ 1. Событие, вероятность которого равна нулю, называются невозможным, а то, вероятность которого равна единице, – достоверным.

Такой способ определения вероятности называют эмпирическим, он требует проведения большого числа испытаний или наблюдений. В некоторых случаях без него невозможно оценить вероятность того или иного события. Например, для того чтобы узнать вероятность того, что 1 июня следующего года будет солнечный день, необходимо взять результаты метеорологических наблюдений для 1 июня за многие десятки лет, найти, сколько раз в этот день была ясная погода, и разделить это число на количество лет, в течение которых проводились наблюдения.

Однако во многих случаях вероятность события можно определить, не проводя испытаний, на основе только теоретических рассуждений. У нас нет никаких оснований думать, что шестёрка, как и любое другое число очков, будет выпадать чаще других. Поэтому можно заранее утверждать, что вероятности выпадения всех шести возможных вариантов равны между собой и, следовательно, равны 1/ 6. Если мы вытаскиваем наугад карту из полной колоды, то вероятность того, что она будет червовой, равна j, точно такой же, как и для любой другой масти. Если мы много раз будем вынимать по карте (назовём это действие испытанием), а затем каждый раз возвращать её обратно и перетасовывать колоду, то результат достаточного количества испытаний будет такой: 1/ 4червей, 1/ 4бубен, 1/ 4треф и 1/ 4пик. Если же результат окажется иным, то это будет означать, что масти в колоде находятся не в равном количестве, т. е. что колода «неправильная».

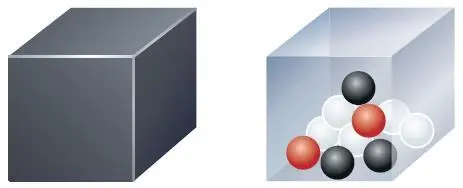
Рис. 196. Урна с шарами (пояснения в тексте)

Точно так же, если на игральной кости какое-то число будет выпадать чаще или реже, чем в одной шестой случаев, мы можем быть уверенными, что кость бракованная. Если все возможные события имеют одинаковые вероятности, их называют равновероятными. Если число таких событий равно N, то вероятность каждого из них равна 1/N.

Однако далеко не всегда мы имеем дело с равновероятными событиями, можно даже сказать, что чаще бывает наоборот. Рассмотрим простой пример. У нас есть ящик (в теории вероятности он называется урной), в котором находится 10 тщательно перемешанных шаров, из которых 5 белых, 3 чёрных и 2 красных (рис. 196). Вынем наугад один шар. Спрашивается, какова вероятность извлечь шар определённого цвета? Очевидно, что мы имеем 5 шансов из 10 вынуть белый шар, 3 – чёрный и 2 – красный, т. е. вероятности вынуть белый, чёрный и красный шар равны, соответственно, 0,5, 0,3 и 0,2. События, заключающиеся в извлечении белого, чёрного или красного шара, называют несовместимыми, так как невозможно, чтобы вынутый шар был одновременно белым и красным.