Лиза Рэндалл - Достучаться до небес: Научный взгляд на устройство Вселенной

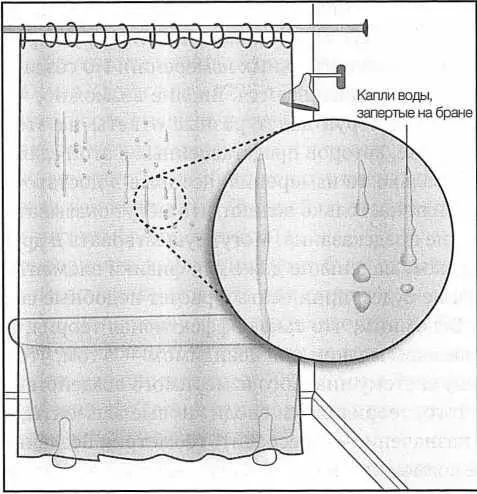
РИС. 62. Брана захватывает в ловушку частицы и силы, которые могут двигаться вдоль нее, но не в состоянии ее покинуть — примерно как капли воды на занавеске в душе

РИС. 63. Открытая струна с двумя концами и замкнутая бесконечная струна

Теория струн предполагает, что существует множество типов бран, но для моделей, пытающихся разрешить проблему иерархии, больше всего интересны те, что распространяются на три измерения — те самые три физических измерения пространства, которые нам известны. Частицы и силы могут быть заперты на такой бране, при том что пространство и тяготение охватывают больше измерений (на рис. 64 схематично представлен мир браны, где человек и магнит ограничены измерениями браны, а гравитация действует как на ней, так и за ее пределами).

Дополнительные измерения теории струн в принципе могли бы оказывать физическое влияние на наблюдаемый мир, как и трехмерные браны. Возможно, важнейшая причина рассматривать дополнительные измерения заключается в том, что они могут влиять на видимые явления и, в частности, объяснять серьезнейшие загадки, такие как проблема иерархии в физике элементарных частиц. Дополнительные измерения и браны могут оказаться ключом к решению этой проблемы; возможно, они помогут понять, почему гравитация так слаба.

Это возвращает нас к главной причине обращения к многомерным моделям и дополнительным пространственным измерениям. Они могут оказывать влияние на явления, в которых мы сейчас пытаемся разобраться, и если это так, то не исключено, что доказательства их существования появятся в самом ближайшем будущем.

Напомню, что проблему иерархии можно сформулировать двумя разными способами. Можно описать суть вопроса тем, что масса хиггсовой частицы — и, соответственно, масштаб слабого взаимодействия — на много порядков меньше массы Планка. Именно этот вопрос мы рассматривали, говоря о суперсимметрии и тех- ницветной силе. Но можно задать и эквивалентный вопрос: а почему гравитация так слаба по сравнению с другими известными фундаментальными взаимодействиями? Сила тяготения определяется планковским масштабом — громадной массой, в десять тысяч триллионов раз превышающей массу слабого взаимодействия. Чем больше масса Планка, тем слабее сила тяготения. Только когда масса объектов достигает или почти достигает планковского масштаба, сила тяготения становится существенной. А до тех пор пока частицы намного легче и не подходят под масштаб, заданный массой Планка (как, собственно, и обстоит дело в нашем мире), сила тяготения остается чрезвычайно слабой.

РИС. 64. Частицы и взаимодействия Стандартной модели могут быть заперты в мире браны, существующей в многомерном пространстве. В этом случае все вокруг — мои знакомые, вещество и известные нам звезды, взаимодействия, такие как электромагнетизм, наша Галактика и Вселенная — существует в привычных трех измерениях. Гравитация, с другой стороны, распространяется на все пространство. (Фото публикуется с разрешения Марти Розенберга.)

Загадка, связанная со слабостью гравитационных сил, по существу эквивалентна проблеме иерархии — решение одной решает и другую. Но формулировка проблемы иерархии в терминах гравитации помогает думать о решениях, связанных с дополнительными измерениями. А нам пора познакомиться с парой наводящих вопросов.

С того самого момента, когда человек впервые задумался над проблемой иерархии, физики были уверены, что решение этой проблемы должно быть связано с модифицированными взаимодействиями частиц на масштабе слабого взаимодействия, то есть на энергиях порядка 1 ТэВ. С учетом только частиц Стандартной модели квантовый вклад в массу частицы Хиггса попросту слишком велик. Должен найтись фактор, который вмешается и «укротит» большие квантово–механические поправки к массе хиггса.

Суперсимметрия и техницвет — два примера моделей, где в высокоэнергетических взаимодействиях могут участвовать новые тяжелые частицы, которые компенсируют ненужные добавки или вообще не дадут им возникнуть. До 1990–х гг. все предлагавшиеся решения проблемы иерархии попадали в одну и ту же категорию — моделей с новыми частицами и взаимодействиями и даже новыми симметриями, проявляющимися на масштабе энергий слабого взаимодействия.

В 1998 г. Нима Аркани–Хамед, Савас Димопулос и Гия Двали предложили альтернативный подход к проблеме. Они указали на то, что поскольку проблема касается не только масштаба слабого взаимодействия, но и его соотношения с масштабом Планка, связанным с гравитацией, то, может быть, все дело в некорректном понимании фундаментальной природы гравитации.

Они предположили, что на самом деле среди масс не существует никакой иерархии — по крайней мере по отношению к фундаментальному масштабу гравитации в сравнении со слабым масштабом. Может быть, в многомерной Вселенной сила тяготения сильна, а в нашем мире с количеством измерений «три–плюс- один» ее измерение дает такой слабый результат только потому, что она как бы «размазана» по всем измерениям. Их гипотеза состояла в том, что на самом деле в многомерной Вселенной гравитация становится сильной на масштабе масс слабого взаимодействия, а при измерениях мы получаем такие скромные результаты не потому, что гравитация фундаментально слаба, а потому лишь, что она, помимо трех привычных измерений, распространяется на большие невидимые измерения.

Чтобы это понять, представьте себе поливальный шланг. Если вода разбрызгивается только в привычных измерениях, то эффект будет зависеть от количества воды в емкости и расстояния от разбрызгивателя до цели. Но если измерений на самом деле больше трех, то вода по выходу из шланга распределится на все эти измерения. Мы на заданном расстоянии от источника увидим намного меньше воды, потому что часть ее уйдет в другие измерения, видеть которые мы не можем (такая ситуация схематически изображена на рис. 65).

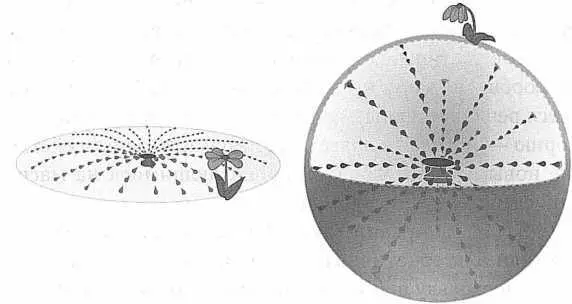
РИС. 65. В многомерном пространстве сила взаимодействия слабеет быстрее, чем в пространстве с меньшим числом измерений. Ситуация аналогична разбрызгиванию воды в многомерном разбрызгивателе, где вода расходится намного быстрее, чем в обычном трехмерном. Вода быстрее расходится по трем измерениям, чем по двум, — на рисунке воды хватает только тому цветку, который получает ее из двумерного, а не трехмерного разбрызгивателя