Пол Стейнхардт - Невозможность второго рода. Невероятные поиски новой формы вещества

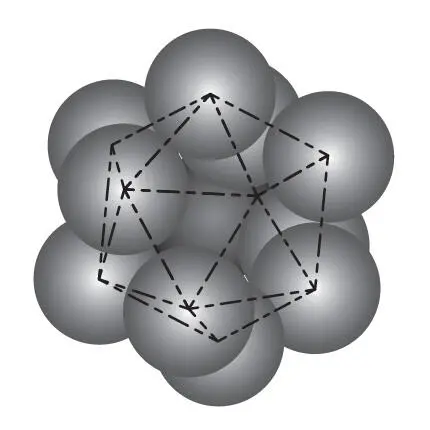
Затем мы попытались окружить этот первый икосаэдр еще двенадцатью такими же икосаэдрами, построив более крупную и сложную структуру – “икосаэдр из икосаэдров”. Но это сразу же привело к новой проблеме. Икосаэдры не прилегают плотно друг к другу – между ними остаются большие зазоры. Поэтому мы попытались сохранить структуру, вставляя дополнительные пенопластовые шарики и куски проволоки, чтобы заполнить все пустые пространства между отдельными икосаэдрами. Этот метод неплохо работал и позволил нам построить большой кластер с симметрией икосаэдра, содержащий более 200 атомов.

Затем мы попытались повторить наш успех, используя на сей раз тринадцать копий этого большого кластера, чтобы построить из них еще более крупный. Однако теперь и просветы получались намного больше – и модель постоянно разваливалась на части.

Наш нехитрый поделочный проект, по-видимому, демонстрировал фундаментальное ограничение в создании атомных структур с икосаэдрической симметрией. Поскольку отдельные икосаэдры не прилегают плотно друг к другу, между ними с добавлением атомов появляются все более крупные просветы, которые требуется как-то заполнять. На основе этого опыта мы предположили, что икосаэдрическую симметрию невозможно распространить более чем на несколько сотен или, возможно, тысяч атомов.

Мы с Довом ошибочно считали, что наша стратегия иерархического построения – от одного кластера к кластеру кластеров – это единственный способ сохранения икосаэдрической симметрии. По сей день я храню в кабинете одну из тех каркасных моделей в качестве напоминания о том, как близки мы были к ошибочному выводу.

Мы вдвоем обдумывали публикацию статьи с описанием нашего вывода о невозможности икосаэдрической симметрии. Однако Дов спас нас от позора, принеся статью о замощениях Пенроуза, опубликованную четырьмя годами ранее в Scientific American . Пенроуз? Я, конечно, хорошо знал это имя. Но оно совершенно точно не ассоциировалось у меня с какими-либо формами вещества или геометрическими замощениями.

Роджер Пенроуз (ныне сэр Роджер Пенроуз), физик из Оксфордского университета, уже тогда был известен всему миру своим вкладом в общую теорию относительности и ее применением к пониманию эволюции Вселенной. В 1960-х годах Пенроуз доказал ряд важных теорем о сингулярности, показывающих, что в широком диапазоне условий Вселенная, расширяющаяся в наши дни, должна была появиться в результате Большого взрыва. Спустя более чем четыре десятилетия некоторые космологи, включая меня, рассматривают способы обойти эти начальные условия, с тем чтобы избежать Большого взрыва и заменить его Большим отскоком.

Нам крупно повезло, поскольку единственная причина, по которой Дов знал о замощениях Пенроуза, состояла в том, что он первоначально пришел в Пенн работать как раз в области общей теории относительности. В декабре 1980 года, за год до того, как попасть на мою лекцию, он слышал, как Пенроуз рассказывал о своих схемах замощения на международной конференции.

Дов был участником Десятого техасского симпозиума по релятивистской астрофизике. Для мероприятия, проходившего в Балтиморе, который находится примерно в двух тысячах километров от Далласа, название было довольно странное. Тут сказалось следование неформальной традиции. Техас принимал первый симпозиум по релятивистской астрофизике, и поэтому все последующие сохраняют это первоначальное название, даже если проводятся в швейцарской Женеве.

В кулуарах конференции между научными докладами Дов наткнулся на Роджера Пенроуза, беседующего с группой студентов. Надеясь узнать что-нибудь о последних работах Пенроуза по теории относительности, он подошел ближе и прислушался к разговору.

К немалому его удивлению, Пенроуз говорил вовсе не о теории относительности или космологии. Вместо этого он рассказывал студентам о новой схеме замощения, которую придумал несколькими годами ранее просто ради развлечения. По сути, он открыл ее, просто машинально рисуя на бумаге. Пенроуз набрасывал в блокноте схемы плиток и их групп, пока не обнаружил замощение, позволявшее решить знаменитую математическую головоломку. Он был не только безгранично любопытным творческим гением, но также и чрезвычайно талантливым художником, способным рисовать от руки точные фигуры. На протяжении всей своей карьеры Пенроуз часто использовал на своих семинарах замысловатые рисунки для пояснения сложных математических вопросов.

Придумывание нового типа замощения может показаться странной формой забавы. Для Пенроуза это было упражнением в “развлекательной математике”, хобби, состоящим в исследовании некоторых хорошо известных математических проблем и головоломок. Этим занимаются самые разные люди от начинающих любителей до знаменитых математиков, от молодежи до стариков.

Самым известным автором в жанре развлекательной математики в то время был Мартин Гарднер, который на протяжении двадцати пяти лет вел в Scientific American ежемесячную колонку “Математические игры”.

Статья, которую принес мне Дов, как раз и была колонкой Мартина Гарднера в Scientific American , посвященной замощениям Пенроуза и опубликованной в 1977 году, примерно через три года после изобретения Пенроузом этих замощений. В статье рассказывалось, как Пенроуз обнаружил изящное решение проблемы, над которой много лет бились любители развлекательной математики: можно ли найти такой набор плиток, который покрывает пол без зазоров, причем только непериодически ?

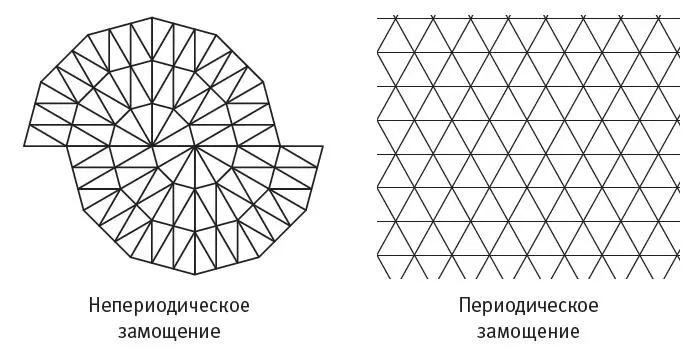
Треугольниками можно покрыть пол не периодически, если, например, расположить их в форме спирали, как показано на иллюстрации внизу слева. Однако из треугольников можно также выстроить периодическое замощение, показанное внизу справа. Поэтому треугольники не являются решением поставленной задачи.

Когда-то математики считали, что невозможно найти фигуру или комбинацию фигур, которая будет удовлетворять этим требованиям. Однако в 1964 году математик Роберт Бергер сконструировал корректный пример, в котором использовалось 20426 различных форм плиток. С течением времени другим удалось найти примеры с использованием намного меньшего числа плиток различной формы.

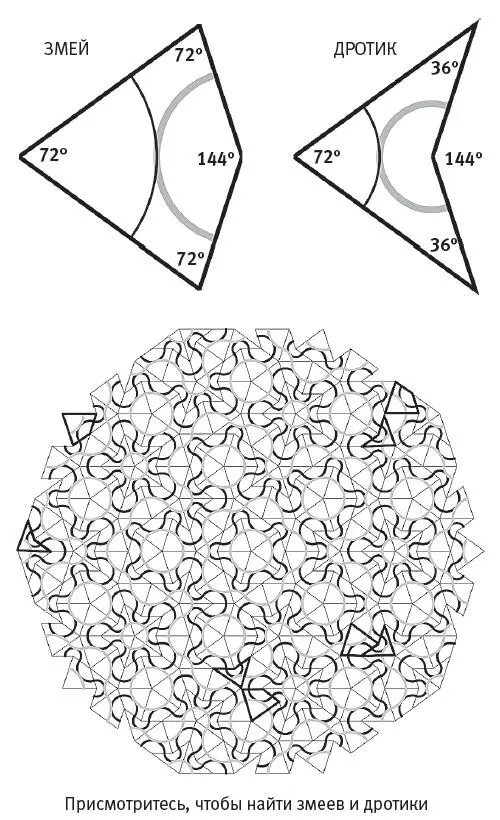
В 1974 году Пенроуз совершил большой прорыв, когда нашел решение задачи с использованием всего двух плиток разной формы, которые он назвал “змеями” и “дротиками” ( kites и darts ; см. вверху). На каждой из этих плиток нарисована дуга окружности, или “лента”. Пенроуз ввел правило, согласно которому две плитки можно прикладывать друг к другу сторонами, только если ленты на обеих сторонах общего ребра состыковываются. Следование этому “правилу совмещения” не позволяет плиткам складываться в какой-либо регулярно повторяющийся рисунок. Замощение, представленное выше, демонстрирует сложный рисунок, образуемый лентой, когда много змеев и дротиков прикладываются друг к другу в соответствии с пенроузовским правилом совмещения.