Александр Матанцев - Тайны римских додекаэдров в разные эпохи

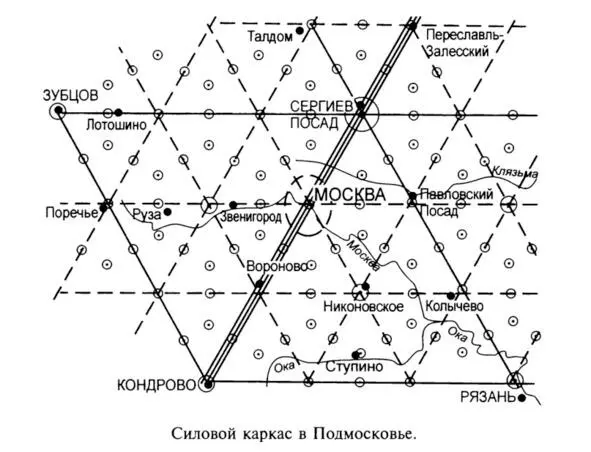
Рис. 10

Рис. 10. Силовой каркас в Подмосковье [93]

Большую часть Московской области занимают два треугольника 4-й подсистемы с длиной сторон 195 км, их вершины – у г. Зубцова Тверской области, чуть южнее Сергиева Посада, у Кондрова Калужской области, севернее Рязани; их центры – в 13 км западнее Звенигорода и у села Никоновское Раменского района. Район вблизи Сергиева Посада является весьма примечательным по энергетике, и, кроме того, там выявляется кольцевая ландшафтная структура диаметром 60 км. А в системе 5-го порядка расстояние между центрами треугольничков оказывается равным 60 верстам, то есть соответствует старой русской мере длины – «конке» [93]. Прекрасно согласуясь с этой мерой и «шагом» системы 5-го порядка, на одной прямой последовательно расположены древние русские города – Москва, Сергиев Посад (ранее Загорск, ещё ранее Троица, а до этого там находилось святилище «Белые боги»), Переславль-Залесский (где находился «синий камень» – место поклонения племён меря и веси), Ростов Великий (там было святилище Велеса), Ярославль, а сама эта прямая совпала с ребром первой подсистемы. Поделим рёбра этих треугольников на три части, соединим и получим в каждом из них по девять треугольников 5-й подсистемы (пунктир на схеме). Их вершины (диаметром 3—4 км) приходятся на древний центр Москвы, южнее Воронова Подольского района, южнее Павловского Посада, севернее Талдома, южнее Пущина, вблизи Вышегорода Наро-фоминского района (здесь валы городища-крепости XIV века), северо-восточнее Сенежского озера и др. Центры этих треугольников лежат юго-восточнее Подольска, восточнее Спаса Волоколамского района, вблизи Ступина, южнее Орудьева Дмитровского района и др.

Существенный элемент в поисковую работу внесли сообщения о найденных археологами так называемых «странных предметах» в форме додекаэдра непонятного назначения (рис. 11). В центрах граней предметов – отверстия, в вершинах – сферические выпуклости. При соединении центров треугольников построенной системы получается именно такой же додекаэдр – правильный 12-гранник с пятиугольными гранями. Возникло предположение, что «странный предмет» – модель силовой системы (с различными функциями в вершинах и центрах граней), вместе с икосаэдром составляющий силовой каркас Земли. Совмещение на глобусе икосаэдра и додекаэдра и дало модель (ИДСЗ), показано на рис. 11.

Рис. 11

Рис. 11. Странные предметы IV века. Тела Платона: тетраэдр (А), гексаэдр (Б), октаэдр (В), додекаэдр (Г), икосаэдр (Д) [90]

Проведено сопоставление многих общепланетарных явлений, процессов и структур с узлами и рёбрами ИДСЗ. Оказалось, что Русская, Сибирская, Африканская древние геологические платформы, Канадская и Гренландская части Северо-Американской платформы, а также все три части Антарктической платформы (разделённые понижениями) территориально совпадают с треугольными гранями икосаэдра, а разделяющие платформы геосинклинальные области (подвижные пояса земной коры) идут вдоль рёбер между ними. В 80-х годах прошлого века сопоставлять Землю с додекаэдром предлагал Фай. В 1929 году идеи Бомона дополнил и развил советский исследователь С. И. Кислицын, который проводил сравнения своих геометрических построений, в том числе додекаэдра и икосаэдра, с залежами некоторых полезных ископаемых: нефти, алмазов. Советские профессора Б. Л. Личков и И. И. Шафрановский в 1958 году сопоставили форму Земли с октаэдром, позднее геолог В. И. Васильев – с додекаэдром, а Вольфсон – с кубом.

Итак, 20 районов планеты (вершины додекаэдра) – центры потоков восходящего вещества, а 12 районов (вершины икосаэдра) – центры нисходящих потоков. Общее количество конвективных ячеек – 60. Зонами восходящего вещества земная кора как бы стягивается в 12 равных структурных «плит», то есть поверхность планеты стремится приобрести симметрию додекаэдра(рис. 12).

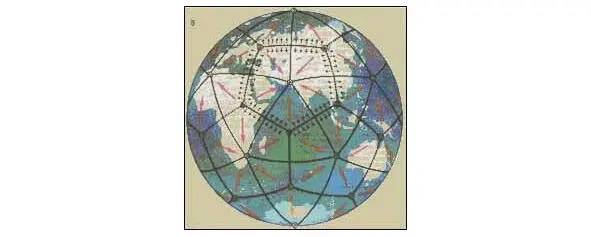
Рис. 12

Рис. 12. Механизм горизонтального перемещения вещества земной коры согласно ИДСЗ на примере формирования «Пакистанской» плиты.

К. А. Лачугин[93]. Земную поверхность в течение многих веков сравнивали с тетраэдром, кубом, октаэдром, икосаэдром, додекаэдром, обычно исходя из наблюдаемого её геометризма. Первыми в этой работе были, по-видимому, Пифагор, Платон и Архимед, которые изучали даже не столько Землю, сколько общую структуру всего мироздания. В своё время Пифагор отождествил Вселенную с космосом и таким образом перенёс на неё древнегреческое определение космоса как «порядка, надлежащей меры, прекрасного устройства». Математическими моделями, воплощающими в себе такие же понятия, у пифагорейцев, а затем и у Кеплера, были правильные многогранники, получившие название «тел Платона». Существует всего пять правильных выпуклых многогранников, получивших название «тел Платона»: тетраэдр, куб, октаэдр, икосаэдр, додекаэдр.

Рис. 13

Рис. 13. Тела Платона [93]

Додекаэдру у Платона отведено очертание Вселенной и очертание Земли как планеты [93]. В своём сочинении «Федон» он писал: «Земля, если взглянуть на неё сверху, похожа на мяч, сшитый из двенадцати кусков кожи и пёстро расписанный разными цветами. Краски, которыми пользуются наши живописцы, могут служить образчиками этих цветов, но там вся Земля играет такими красками, и даже куда более яркими и чистыми». Эти знания Платон вполне мог позаимствовать у пифагорейцев, ибо уже у них бытовало мнение, что сфера Вселенной возникла из додекаэдра. Многие свои знания пифагорейцы считали необходимым держать в тайне. Один из них, Гиппас, разгласил одну из тайн, первым начертив шар, покрытый двенадцатью равными пятиугольниками.

[74].Римский додекаэдр – это правильный многогранник из двенадцати пятиугольных плоских граней. Различные экземпляры римских додекаэдров были отлиты из бронзы и украшены шарообразными ручками на всех вершинах или угловых точках пятиугольников. У большинства додекаэдров в центре плоских граней были вырезаны круглые отверстия. На одних экземплярах отверстия одинаковые, на других разных диаметров. Прошло более двух столетий со времени обнаружения первых додекаэдров, но исследователи так и не разгадали возможные функции. Римские додекаэдры имели особую ценность для их владельцев. Их находили среди кладов, монет, драгоценностей и редких предметов.