Юрий Трифонов - Властелин механики. 7 великих законов в понятном изложении

Если же речь идёт про сжатую пружину, то схема расчёта слегка иная.

Здесь есть деформация пружины x и жесткость пружины k.

Хотя формула и похожа на расчет кинетической энергии, но тут мы имеем абсолютно другой физический смысл . Экспериментальные исследования позволили выяснить, что энергии будет вот столько, но факт того, что величины считаются похожим образом ни о чем не говорит. В одном случае происходит движение со скоростью, а в другом случае есть внутренние взаимодействия в теле, которые вызывают явление упругости.

Кстати говоря, сжатая пружина как нельзя лучше подходит для демонстрации явления потенциальной энергии. Глядя на неё не сложно понять всю суть рассматриваемой проблемы. Мы сжали пружину и пока она находится в таком состоянии, внутренние силы стараются её распрямить. Стоит её отпустить, и пружина отлетит в лоб. Вспомним шутку из Симпсонов, когда Гомер открыл банку от чипсов и оттуда в глаз ему вылетела пружина, с которой он потом бегал по городу. Это и была потенциальная энергия, превратившаяся в кинетическую.

Рис. 16. Сжатая пружина может отлететь в глаз

Всегда, когда речь заходит о кинетической энергии, мы имеем дело с движением. Не случайно кинетическая энергия рассчитывается по формуле:

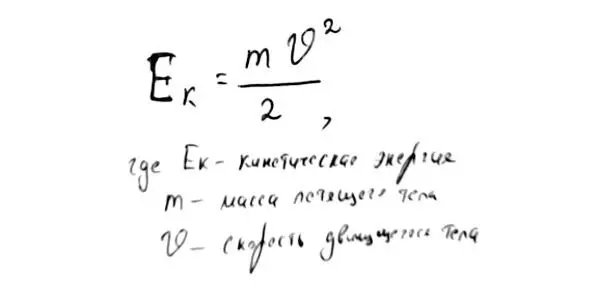
В расчёте участвует скорость, которая обозначена тут буквой V. Само собой, масса (m) тоже будет присутствовать в этом расчёте. Ведь чем массивнее тело, тем сильнее оно может ударить или, говоря научным языком, тем большее количество энергии оно может запасти при движении с некоторой скоростью.

Ну и анализируя теперь пример с рукой и столом, который был в самом начале обсуждения, мы можем провести более глубокий анализ процесса.

Пока рука приближалась к столу, присутствовала кинетическая энергия, которая в итоге была передана столу и вызвала его незначительную деформацию. Несколько миллисекунд, пока стол не вернулся к своей исходной форме, он обладал потенциальной энергией. Сразу произошло несколько интересных процессов — один вид энергии превратился в другой вид энергии, а ещё сработал закон сохранения энергии .

Пример, вероятно, не самый полный и может показаться, что мы попросту забыли о некоторых моментах. Скажем, мы не учли, что деформируется и сама рука. Но в физике принято исключать малозначимые факторы и процессы или пренебрегать ими .

Строится принципиальная схема, а некоторые объекты вполне можно принимать за материальные точки, недеформируемые тела и делать прочие упрощения. Таких допущений огромное количество. Они есть в каждом учебнике при разборе ситуаций. Ведь не внеси мы такое упрощение и самая простая задачка про брусок и наклонную плоскость будет решаться этак на 100 страницах!

В случае с рукой мы исключили множество моментов – стол нагрелся от удара, рука тоже деформировалось, насколько бы это не было сложным для беглого восприятия, но у движущегося тела присутствовала и потенциальная энергия и многие другие. Мы всё это упрощаем для того, чтобы сосредоточиться на основном явлении.

Но! Это не означает, что все остальные факторы пропали вовсе! Они есть. Мы понимаем, что их влияние минимальное и отбрасываем их. Если же считать «по уму», то следует проводить сложнейшие интегральные вычисления и схемку рисовать покруче. Подобные вычисления потребуются, разве что, при проектировке самолета.

Из этих нехитрых примеров следует, что при механических воздействия энергия может неограниченное количество раз превращаться из одного вида в другой . Потенциальная энергия переходит в кинетическую, а кинетическая переходит в потенциальную.

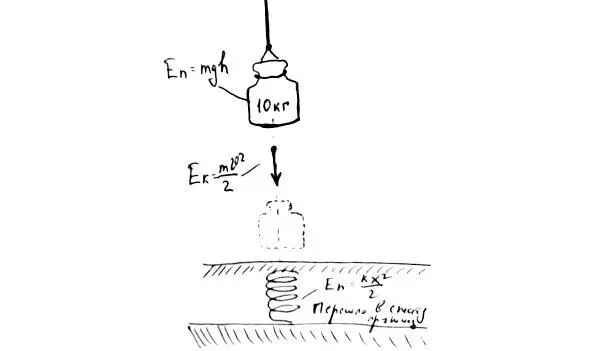
Рис.17. Превращение энергии при падении гири на пружинный пол

Когда речь идёт о механической энергии всегда рассматривается сумма механической и потенциальной энергий. Это будет так называемая полная энергия системы.

Рассуждения о превращении энергии подталкивают к мысли, что на самом-то деле энергия не появляется и не пропадает. Она просто превращается из одной формы энергии в другую с потерями на другие процессы. И мы пришли к закону сохранения механической энергии .

Закон сохранения энергии гласит, что энергия ниоткуда не возникает и никуда не пропадает. Энергия лишь переходит из одного вида в другой или от одного тела к другому.

Как вы заметили, слово «механической» тут отсутствует. Закон справедлив не только для механики. Как и понятие «энергия» закон сохранения значим для всей физики сразу вне зависимости от раздела. Он работает во всей вселенной.

Но применительно к механике закон сохранения энергии учитывает преимущественно кинетическую энергию тела, потенциальную энергию тела и иногда ещё внутреннюю энергию тела (если происходит передача энергии движения в нагрев и т.п.), о которых мы поговорили чуть выше.

Теперь посмотрим, как сформулирован закон сохранения механической энергии в учебниках:

В замкнутой и консервативной системе тел полная механическая энергия сохраняется: ΔЕ = 0

или Е потенциальная 1 + Е кинетическая 1 = Е потенциальная 2 + Е кинетическая 2

или как вы это привыкли видеть:

Почему замкнутой? Потому что если система не замкнутая, то она будет обмениваться энергией с другими участниками процесса, и энергия в итоге рассеивается. Тот самый пример со столом подходит как нельзя лучше.

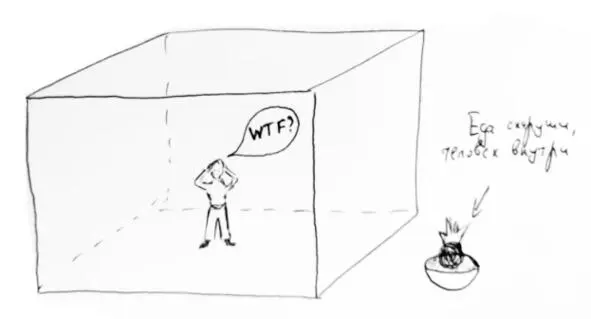
Рис.18. Человек, закрытый в ящике – это замкнутая система

Скажем, запустили мы всем известные шарики для демонстрации закона сохранения импульса. Они качаются и передают друг другу энергию в одной замкнутой системе.

Рис.19. Постоянная передача энергии с её превращением в замкнутой системе