Мэтью О. Джексон - Человеческие сети. Как социальное положение влияет на наши возможности, взгляды и поведение

Говоря о несоразмерном присутствии, я имею в виду важное явление, известное как “парадокс дружбы”; на него указал в 1991 году социолог Скотт Фелд {11} 11 Feld (1991). .

У вас никогда не возникало впечатления, что у других людей друзей намного больше, чем у вас? Если возникло, вы не одиноки. В среднем друзей у наших друзей действительно больше, чем у любого типичного представителя населения. Это и есть парадокс дружбы.

На рисунке 2.1 мы видим парадокс дружбы в сети дружеских связей среди старшеклассниц; этот пример взят из классической работы Джеймса Коулмана {12} 12 Coleman (1961). . Здесь представлены четырнадцать девочек. Для девяти из них верно утверждение, что у их подруг в среднем больше подруг, чем у них самих. У двух – то же количество подруг, что и у их подруг в среднем, и лишь три девочки пользуются большей популярностью, чем их подруги в среднем {13} 13 Это всего два компонента (связанных куска) сети. Более широкая сеть, не изображенная здесь, выявляет тот же феномен. У 146 девочек есть подруги (имеется в виду взаимная дружба). Из них у 80 имеется меньше подруг, чем в среднем у их подруг, у 25 – то же количество подруг, что и у их подруг, а у 41 девочки – больше подруг, чем у их подруг. .

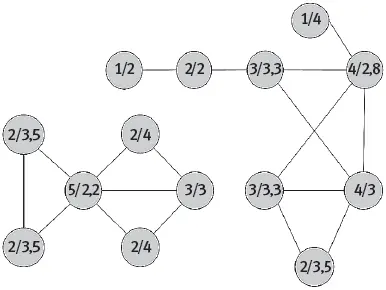
Рис. 2.1. Парадокс дружбы. Данные из исследования Джеймса Коулмана 1961 года, посвященного школьной дружбе. Каждый узел (кружок) обозначает девочку, а звено между ними указывает на дружбу между двумя девочками. Парадокс заключается в том, что большинство девочек оказываются менее популярными, чем их подруги. Первое из чисел, присвоенных каждой девочке, означает количество ее подруг, а второе – среднее количество подруг, имеющихся у ее подруг. Например, у девочки в нижнем левом углу две подруги, а у этих подруг – 2 и 5 подруг, что в среднем дает число 3,5. Таким образом, 2/3,5 означает, что сама она пользуется меньшей популярностью, чем ее подруги в среднем. То же самое верно для 9 из 14 девочек, и лишь 3 более популярны, чем их подруги, а 2 равны по популярности своим подругам.

Парадокс дружбы легко понять. Наиболее популярные личности оказываются в друзьях у очень многих людей, а имеющие мало друзей, естественно, фигурируют в числе друзей у сравнительно меньшего количества людей. Люди, имеющие множество друзей, присутствуют слишком часто среди чьих-то друзей относительно их собственной доли в населении, тогда как люди, имеющие очень мало друзей, напротив, присутствуют там слишком редко. Человека, имеющего десятерых друзей, считают своим другом вдвое больше людей, чем другого человека, у которого друзей всего пять.

В математическом смысле этот парадокс лишен особой глубины – впрочем, как и большинство парадоксов. Вместе с тем он дает о себе знать почти во всех наших взаимодействиях. Каждый, кому довелось быть родителем – да даже и ребенком! – наверняка не раз слышал фразы: “у всех остальных в школе есть…” или “всем остальным в школе разрешают…”. Хотя подобные утверждения, как правило, и лживы, они часто отражают наши ощущения. С наиболее популярными учениками ведь дружат очень многие дети, и потому если у этих всеобщих любимчиков появляются одинаковые увлечения, тогда остальные дети приходят к выводу, что этим увлекаются абсолютно все. Популярные люди непропорционально часто определяют представления других и задают нормы поведения для остальных.

Чтобы понаблюдать за последствиями парадокса дружбы в самом наглядном виде, давайте рассмотрим один-единственный пример, а потом обратимся к кое-каким данным для подкрепления этого примера.

Рассмотрим школьный класс, где на учеников влияют друзья {14} 14 Чтобы увидеть похожие примеры, иллюстрирующие тенденциозную оценку мнений, см.: Lerman, Yan, and Wu (2015). Еще можно найти примеры в популярных блогах (см., напр., Kevin Schaul, Washington Postblog от 9 октября 2015 года, “A Quick Puzzle to Tell Whether You Know What People Are Thinking”); и эксперименты, проведенные Kearns, Judd, Tan, и Wortman (2009). . В глубине души эти ученики – конформисты. Перед ними стоит простой выбор: что носить – однотонный костюм или костюм в клетку? У каждого свои предпочтения, и в первый день учебного года каждый одевается, следуя собственному вкусу, что и показано на рисунке 2.2.

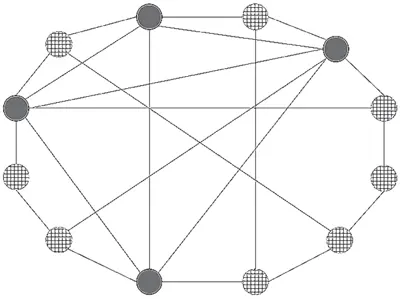
Рис. 2.2. Первый день учебного года. Четыре самых популярных ученика предпочитают однотонные костюмы; остальные восемь предпочитают костюмы в клетку.

Как истинные конформисты, ученики хотят делать то, что делает большинство остальных, и следуют собственным предпочтениям только в том случае, если сторонников обоих стилей насчитывается поровну. Как видно из рисунка 2.2, четверо учеников предпочитают однотонные костюмы, а восемь – костюмы в клетку. Таким образом, клетке отдают предпочтение две трети учеников, и если бы они сами могли увидеть предпочтения всей группы, тогда уже на следующий день все явились бы в костюмах в клетку. Однако отметим, что однотонные костюмы больше нравятся четырем самым популярным – возможно, самым смелым – ученикам.

Ученики видят не всех – они взаимодействуют в основном со своими друзьями, на что и указывают звенья между узлами сети.

Рисунки 2.3 – от (a) до (d) – показывают, чтó происходит в каждый из следующих дней. Все популярные ученики видят друг друга и некоторых других, и все они видят, что большинство носит однотонное, и потому продолжают ходить в однотонном. Некоторые другие ученики видят главным образом популярных учеников, и потому они тоже переодеваются в однотонное. Как мы видим на схеме 2.3 (а), популярные ученики продолжают носить однотонное, и их примеру следуют еще четверо учеников, и ко второму дню у нас уже восемь учеников в однотонных костюмах. Начиная с этого момента намечаются стремительные перемены, что мы видим на схемах от (b) до (d). С каждым днем все больше учеников, по-прежнему одетых в клетчатое, видят, что большинство их друзей приходит в однотонном, и сами тоже переодеваются в однотонное. К пятому дню уже все ученики в классе одеты в однотонное – и это несмотря на то, что вначале большинство из них отдавало предпочтение клетчатому.

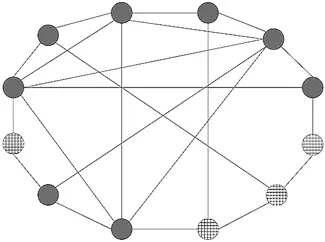
(а) 2-й день, четыре человека решили одеться так же, как самые популярные ученики.

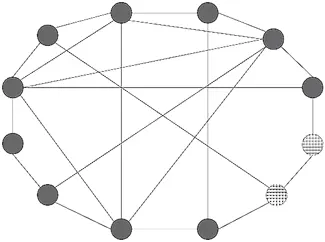
(b) 3-й день, еще больше перебежчиков.

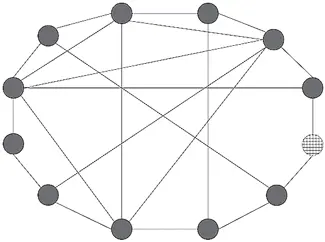
(c) 4-й день, процесс продолжается.