Мэтью О. Джексон - Человеческие сети. Как социальное положение влияет на наши возможности, взгляды и поведение

Это как бы круговое определение: страница “важна”, потому что связана с другими “важными” страницами, которые, в свой черед, оказываются “важными”, потому что связаны с “важными” страницами. Несмотря на этот круговой характер, решение получается красивое – и чрезвычайно полезное для сетевой среды.

Предположим, что нам нужно распространить слух или какую-то информацию, которая, как мы полагаем, будет разноситься путем “сарафанного радио”. Чтобы понять, почему здесь не годится прямолинейный принцип популярности, посмотрите на сеть, изображенную на рисунке 2.5. Даже беглого взгляда на нее достаточно, чтобы заметить, что положения Нэнси и Уоррена сильно разнятся, хотя оба они имеют по двое друзей. Различие состоит в том, что их друзья обладают разным качеством связей, а потому и сами они занимают разное положение в сети. У каждого из друзей Уоррена лишь по два друга, тогда как у друзей Нэнси – семеро и шестеро. Таким образом, пускай Уоррен и Нэнси занимают одинаковое положение с точки зрения “степени” (то есть по количеству друзей), у друзей Нэнси степени выше, чем у друзей Уоррена.

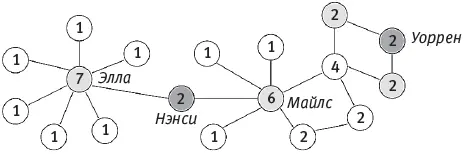
Рис. 2.5. Два человека, Нэнси и Уоррен, обладают степенью 2. Однако они различаются количеством связей их друзей – и потому их абсолютные положения в сети различны.

На этом можно было бы остановиться: вместо того чтобы просто считать друзей, мы могли бы считать, сколько дополнительных друзей “приводит” за собой каждый из этих друзей, – иными словами, подсчитывать друзей друзей – назовем их “друзьями второй степени”. Для начала хорошо было бы не ограничиваться подсчетом непосредственных друзей, а считать еще и их друзей, тогда сразу же видно, что у Нэнси больше возможностей для распространения информации, чем у Уоррена. Но зачем останавливаться на этом? Почему не учесть еще и “друзей третьей степени”? Пускай дружба Нэнси с Эллой и не столь плодотворна, если иметь в виду наличие друзей третьей степени, зато ее дружба с Майлсом ведет к еще большему числу связей. Удалившись от Нэнси на три шага, мы уже охватим всех, кроме Уоррена. Отойдя же на три шага от Уоррена, мы насчитаем дополнительно всего пятерых человек, тогда как, удаляясь от Нэнси, мы насчитали шестнадцать человек. Таким образом, Нэнси – гораздо более перспективный кандидат для распространения информации, чем Уоррен, хотя оба они обладают одинаковой степенью.

Как же выявлять эти качества в большой сети, где можно продолжать такой подсчет до бесконечности? Существуют различные способы, но лучше я опишу самую суть задачи. Давайте начнем с того, что просто учтем количество друзей первой степени (непосредственных). Итак, как мы видим из рисунка 2.5, и Нэнси, и Уоррен получат по 2 балла, поскольку у каждого из них – по два друга. Далее, учтем друзей второй степени. Но должны ли мы наделять их таким же значением, что и друзей первой степени? Например, если мы представим себе, что информация начнет распространяться от Нэнси, то, вероятнее всего, она перейдет от Нэнси к Майлсу, затем к кому-нибудь из друзей Майлса, – поскольку она должна вначале перейти от Нэнси к Майлсу, а затем дальше – уже от Майлса. Пожалуй, менее вероятно, что ей понадобится для распространения два шага, а не один шаг, – скажем, в два раза менее вероятно. Так что пока давайте присвоим другу друга значение вдвое меньшее, чем непосредственному другу. У Нэнси одиннадцать друзей второй степени, поэтому присваиваем ей 11/2 баллов, учитывая количество друзей ее друзей. А у Уоррена имеется только один друг второй степени, поэтому он получает 1/2. Итак, у Нэнси пока что 7,5 балла, если считать ее друзей первой и второй степени, а у Уоррена – только 2,5. Далее мы переходим к подсчету друзей третьей степени: у Нэнси их трое, а у Уоррена – двое. Опять-таки присвоим новым друзьям значение вдвое меньшее по сравнению с предыдущим уровнем, то есть по 1/4. Таким образом, к уже набранным очкам Нэнси прибавится еще 3/4, а к прежним очкам Уоррена – 2/4, после чего общее число баллов у Нэнси уже достигло 8,25, а у Уоррена оно выросло до трех. Продолжая подсчет таким способом, мы сможем количественно оценить, насколько охват людей в сети у Нэнси больше, чем у Уоррена.

Относительное сравнение Нэнси с Уорреном позволяет разрешить и другой вопрос. Давайте условимся, что центральность каждого из них пропорциональна сумме центральностей их друзей. Этот подсчет будет подобен тому, что уже проделан нами ранее. Тем самым Нэнси получит некоторую долю очков Эллы и Майлса – из-за того, что будет учтена некоторая доля очков их друзей, и так далее. Эти повторные операции будут подобными, потому что Элла и Майлс получают очки от своих друзей, которые приходятся друзьями второй степени Нэнси, а те очки получены от их друзей, которые приходятся Нэнси друзьями третьей степени, и так далее {26} 26 Есть и легкое различие – в том, что теперь мы иногда ведем двойной счет: ведь одним из семи друзей Эллы является Нэнси, а значит, мы и саму Нэнси причисляем к друзьям второй степени. На самом деле, такой двойной счет немного облегчает арифметику, так как на каждом этапе нам нужно лишь установить количество связей, но не нужно вспоминать, кого мы уже считали, а кого нет. Влияние двойного счета обсуждается в работе Banerjee, Chandrasekhar, Duflo, and Jackson (2013, 2015). .

По счастью, система уравнений такого типа – когда центральность каждого человека пропорциональна сумме центральностей его друзей – вполне естественная и легкорешаемая математическая задача. Она появилась благодаря ряду научных работ известнейших математиков, живших с XVIII по ХХ век: это Эйлер, Лагранж, Коши, Фурье, Лаплас, Вейерштрасс, Шварц, Пуанкаре, фон Мизес и Гилберт. Гилберт назвал решения подобных задач “айген-векторами”, или “собственными векторами”, и это общепринятое современное название. Неудивительно, что собственные вектора фигурируют во всевозможных областях, от квантовой механики (уравнение Шрёдингера) до алгоритма eigenface, содержащего основные строительные блоки для программ распознавания лиц. Решая задачу собственного вектора в нашем примере, мы приходим к ответу: количество баллов у Нэнси приблизительно в 3 раза больше, чем у Уоррена, что мы и видим на рисунке 2.6 {27} 27 Если вам интересны подробности показателей на рисунке 2.6, то квадраты показателей центральности в сумме дают единицу, так что вектор показателей центральности нормализован в обычном математическом смысле (в соответствии с L2 или с евклидовой нормой). .

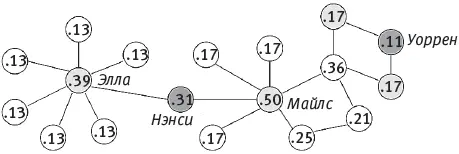
Рис. 2.6. Центральности по собственному вектору для каждого узла (человека). У Нэнси почти в 3 раза больше баллов, чем у Уоррена, хотя у обоих имеется одинаковое количество связей. Больше всего баллов у Майлса, хотя у Эллы наибольшая центральность по степени.