Скотт Пейдж - Модельное мышление. Как анализировать сложные явления с помощью математических моделей

Полагаться на одну модель – это высокомерие, чреватое катастрофой. Верить в то, что одно уравнение может объяснить или спрогнозировать сложные явления реального мира, – значит стать жертвой притягательной силы чистых, строгих математических форм. Не стоит рассчитывать на то, что какая-либо одна модель позволит составить точный численный прогноз уровня моря через 10 000 лет или уровня безработицы через 10 месяцев. Для осмысления сложных систем понадобится множество моделей. Такие сложные системы, как политика, экономика, международные отношения или мозг, демонстрируют непрерывно меняющиеся системные эффекты и закономерности, которые заключены между порядком и хаосом. Сложные явления по определению трудно объяснять, развивать или прогнозировать [9] См. Page, 2010a. .

В результате мы наблюдаем явное несоответствие. С одной стороны, нам нужны модели, чтобы последовательно мыслить, а с другой – любая отдельная модель с несколькими меняющимися элементами не способна объяснить суть сложных многомерных явлений, таких как закономерности в международной торговой политике, тенденции в отрасли потребительских товаров или адаптивная реакция мозга. Никакой Ньютон не сможет написать уравнение с тремя переменными, объясняющее ежемесячные показатели занятости, результаты выборов или снижение уровня преступности. Если мы хотим понять закономерности распространения болезней, изменчивость показателей успеваемости, разнообразие флоры и фауны, воздействие искусственного интеллекта на рынки труда, влияние людей на климат планеты или вероятность социальных волнений, нам следует все это проанализировать с помощью моделей машинного обучения, моделей динамических систем, моделей теории игр и агентных моделей.

Чтобы изложить в общих чертах аргументы в пользу многомодельного мышления, начнем с цитаты поэта и драматурга Томаса Стернза Элиота: «Где мудрость, утраченная нами ради знания? Где знание, утраченное нами ради сведений?». Мы могли бы к этому добавить: где информация, утраченная нами ради данных?

Вопросы Элиота можно формально описать как иерархию мудрости. На ее нижнем уровне находятся данные : первичные, незакодированные события, переживания и явления, такие как рождение, смерть, рыночные сделки, голосование, загрузка музыки, осадки, футбольные матчи и эпизоды видообразования. Данные могут представлять собой длинные цепочки нулей и единиц, временн ы х меток и связей между страницами. В данных нет смысла, упорядоченности или структуры.

Информация описывает данные и делит их на категории. Следующие примеры объясняют различие между данными и информацией. Дождь, падающий вам на голову, – это данные. Общее количество осадков за июль в Берлингтоне, а также уровень воды в озере Онтарио – это информация. Ярко-красный перец и желтая кукуруза в фермерских палатках, расположенных вокруг здания законодательного собрания в Мэдисоне во время субботней ярмарки, – это данные. Совокупный объем реализации продукции фермерских хозяйств – это информация.

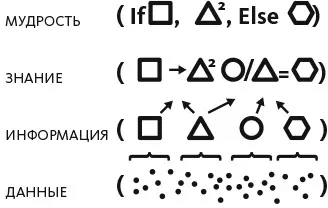
Рис. 1.1.Как модели преобразуют данные в мудрость

Мы живем в эпоху изобилия информации. Полтора столетия назад обладание информацией обеспечивало высокий экономический и социальный статус. Эмма, героиня одноименного романа Джейн Остин, спрашивает, производит ли Фрэнк Черчилл впечатление информированного молодого человека. Сегодня она не стала бы задавать этот вопрос. У Черчилла, как и у всех нас, был бы смартфон. Вопрос в том, как бы он воспользовался имеющейся информацией. В романе «Преступление и наказание» Федор Достоевский пишет: «У нас есть, дескать, факты! Да ведь факты не все; по крайней мере половина дела в том, как с фактами обращаться умеешь!»

Платон определял знание как обоснованное истинное убеждение. В современных определениях оно трактуется как понимание корреляционных, причинных и логических связей. Знание организует информацию и часто принимает форму модели. Экономические модели рыночной конкуренции, социологические модели сетей, геологические модели землетрясений, экологические модели формирования ниш и психологические модели познания – все заключают в себе знание, объясняют и прогнозируют. Модели химических связей объясняют, почему связи в молекулах металла мешают нам просунуть руку сквозь металлическую дверь, тогда как движение молекул воды уменьшает наш вес, когда мы ныряем в озеро [10] Я не приравниваю знания к моделям, а говорю о том, что модели могут отражать знания и обеспечивать надежный способ распространения соответствующих представлений. Термин «знание» имеет множество значений и включает в себя, помимо прочего, такие навыки, как игра в теннис, французкий язык и составление контрактов. Я использую более узкое определение. С более широкой концепцией можно ознакомиться здесь: Adler, 1970. .

На вершине иерархии находится мудрость – способность выявлять и применять соответствующие знания. Мудрость требует многомодельного мышления. Иногда она сводится к выбору лучшей модели, как при извлечении стрелы из колчана. А иногда достигается за счет усреднения моделей, что часто происходит при составлении прогнозов. (Мы обсудим важность усреднения моделей в следующем разделе.) Перед тем как предпринять те или иные действия, мудрые люди применяют несколько моделей, так же как врачи совокупность диагностических тестов. Это позволяет исключить одни действия и отдать предпочтение другим. Мудрые люди и команды выстраивают диалог между моделями, анализируя области их пересечения и различия.

Мудрость может состоять в выборе правильных знаний или модели. Рассмотрим такую физическую задачу: маленькая мягкая игрушка гепарда падает с самолета, летящего на высоте 6000 метров. Чем чревато ее падение на землю? Студент может знать модель гравитации и модель предельной скорости падения. Эти модели рассматривают происходящее под разными углами. Гравитационная модель прогнозирует, что мягкая игрушка пробьет крышу автомобиля. Но модель предельной скорости с учетом сопротивления воздуха говорит о том, что скорость игрушечного гепарда приблизится примерно к 16 километрам в час [11] Это приближенное значение можно получить на основании предельной скорости летящих парашютистов, достигающей почти 320 километров в час. Предельная скорость зависит от массы. Предположим, масса парашютиста в 400 раз больше массы игрушечного гепарда. Квадратный корень из 400 равен 20. Следовательно, предельная скорость игрушечного гепарда равна 320 километрам в час, деленным на 20, или примерно 16 километрам. . Мудрость состоит в знании о том, что следует применить модель предельной скорости. Стоящий на земле человек может поймать мягкую игрушку руками. Как сказал по этому поводу эволюционный биолог Джон Бердон Сандерсон Холдейн, «можно уронить мышь в угольную шахту глубиной в тысячу ярдов; достигнув дна, мышь, отделавшись легким сотрясением, убежит, если только земля будет достаточно мягкой. Крыса погибнет, человек разобьется, а лошадь превратится в лепешку».