Виктор Виноградов - Статьи по общему языкознанию, компаративистике, типологии

4. В практике математического анализа текста нередко прибегают к понятию пространства сообщений, описываемого формулой Е = ( n , U), где U – произвольный алфавит, n – длина слов в U [Шрейдер 1962]. Очевидно, что это пространство является n -мерным. Тогда для любых двух слов ζ и η можно определить расстояние ρ (ζ, η), которое равно числу позиций, в которых слова ζ и η имеют различные символы. Такая интерпретация некоторого текста имеет свои преимущества; единственным ограничением, предполагаемым ею и способным вызвать затруднения при анализе нормального (т. е. специально не пере-кодированного) текста на языке L i , является фиксированность глубины сообщения (под последним понимается слово в U ). Нас интересуют только случаи, когда ρ = 1. Мы будем говорить, что в этом случае имеет место фонологическая оппозиция, реализующаяся в некоторой паре (λ i , λ j ).

Система оппозиций может быть упорядочена также по признаку расстояния, определяемого для точек n -мерного пространства (именно – 12-мерного); однако ввиду невозможности геометрического представления 12-мерного пространства упорядочение фонологических оппозиций может быть достигнуто в несколько этапов путем последовательного перебора нескольких трехмерных пространств. Каждая точка, определяемая тремя координатами, соответствует некоторой фонеме; расстояния между точками суть фонологические оппозиции. Двоичные формулы фонем фиксируют удаленность их друг от друга: расстояние между фонемами φ k и φ i определяется количеством различающихся позиций двоичных символов в формулах этих фонем. Так, если φ k = 001, φ l = 100, то ρ (φ k , φ l ) = 2. В зависимости от того, является ли расстояние между точками минимальным, т. е. равным 1, или нет, оппозиции могут быть разделены на коррелятивные и некоррелятивные. Очевидно, что такая классификация будет отличаться от классификации Трубецкого, данной им в «Основах фонологии» [Трубецкой 1960], тем, что коррелятивные оппозиции, как наиболее важные, оказываются в центре внимания. Именно такого рода классификацию предложил А. А. Реформатский [1961]. В свете сказанного первоначальная классификация оппозиций, отраженная в Проекте 1930 г. (корреляции vs . дизъюнкции), едва ли может быть признана неадекватной.

5.Корреляции составляют фундамент всякой фонологической системы. В соответствии с определением Трубецкого, корреляциями являются одномерные привативные пропорциональные оппозиции. Ж. Кантино, пытаясь дать логическую классификацию оппозиций [Сantinеau 1955], прибегнул к понятию включения, заимствованному из теории множеств. Рассматривая фонемы как множества, Кантино устанавливает для них три типа отношений: включение, пересечение и независимость. В этой системе корреляции трактуются как включения, дизъюнкции – как пересечения или независимости. Интересным моментом в классификации Кантино является анализ так называемых градуальных оппозиций: они попадают в тот же класс, что и привативные, т. е. рассматриваются как включения. В интерпретации Р. О. Якобсона градуальные оппозиции также объединяются с привативными, но они теряют при этом свой характерный признак – градуальность, расщепляясь на две бинарных оппозиции. Ж. Кантино удалось, сохранив их специфичность, представить их как оппозиции, во всяком случае близкие к привативным. На примере вокализма узбекского языка Кантино иллюстрирует свою мысль. Если обозначить, например, i как L + A , где L – передняя локализация, А – минимальный раствор, то е = L + ( А + М ), где М – некоторое количество открытости. Но так как L + A = i , то e = I + M , т. е. i ∈ е . В свою очередь е ∈ æ , так как æ характеризуется по сравнению с е некоторым количеством открытости N : æ = L + ( A + М + N ). Следовательно, i ∈ е ∈ æ . То же можно сказать и о заднем ряде гласных узбекского языка.

Отношение включения представляет в известном смысле иную форму расстояния. Степень включения ξ определяется на численном интервале 0 < ξ < 1. Единица соответствует корреляции, нуль – абсолютной дизъюнкции. Здесь не достигается четкой оппозиции 0 : 1, так как понятия корреляции и дизъюнкции не равномощны: последнее предполагает несколько типов некоррелятивных противопоставлений.

Если определять отношение включения на всем множестве фонем таким образом, что для всяких двух фонем а и b будет известно, что либо а < b , либо b < а (здесь < есть знак строгого содержания), то отношение включения становится отношением частичной упорядоченности для множества (подмножества) фонем и, как всякое отношение частичной упорядоченности, обладает свойствами 1) рефлексивности: а < b. ⊃ .b > а ; 2) транзитивности: а < b. c < а ⊃ .с < b. ; 3) асимметричности: а < b. ⊅ .b < а [Курош 1962: 19].

Определим теперь понятие корреляции. В множестве фонем, рассматриваемом как класс классов, могут быть отмечены такие классы α i и β j , что каждый элемент a ik класса α i находится во взаимно-однозначном соответствии с элементом b jl класса β j . Это отношение назовем коррелятивным и определим следующим образом: отношение является коррелятивным, если никакие два элемента не связаны этим отношением с одним и тем же третьим и ни один элемент не связан этим отношением с двумя другими. Такое определение коррелятивного отношения дает У. Куайн [Quinе 1955: 299]. В символической записи это выглядит так: ( х )( у )( z ) ( xRz. yRz. ∨ .zRx. zRy : ⊃ .x = y ).

Связывая понятие коррелятивного отношения с отношением частичной упорядоченности, мы скажем, что коррелятивным отношением является такое отношение частичной упорядоченности, которое интранзитивно. Вопрос о том, является ли оно рефлексивным, требует особого рассмотрения. Дело в том, что коррелятивное отношение является пропорциональным, как это заметил еще Трубецкой; это свойство позволяет трактовать его как класс пар элементов {a i ; b j }, причем «пара» употребляется здесь в логическом смысле [Quinе 1940: 198 ff.], т. е. как элемент. Это значит, что строевыми элементами фонологической структуры являются не столько фонемы, сколько оппозиции. Такой взгляд может быть обоснован и с точки зрения нейтрализации. Как известно, в фонологии принято называть нейтрализуемыми лишь корреляции; нейтрализация есть такая операция, которая ставит в соответствие двум коррелирующим фонемам некий третий элемент, именуемый архифонемой. Таким образом, имеется некоторое множество архифонем, представляющих собой элементы, каждому из которых взаимно-однозначно соответствует элемент из множества фонем – фонемная пара. Рассмотрение корреляций как фонемных пар отражено, например, в книге С. К. Шаумяна [Шаумян 1962а]. Но если допустить, что корреляция есть логическая пара, то необходимо распространить на корреляции основное свойство пары – некоммутативность: ( a i ; b j ) ≠ ( b j ; a i ). Отсюда следует невозможность равенства a R b = b R a , т. е. невозможность говорить о рефлексивности как свойстве корреляции. Это равенство справедливо лишь в том случае, когда в правой части имеется отношение 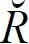, т. е. инверсное но отношению к R . Но такое условие предполагает двойственность (внутреннюю бинарность) коррелятивного отношения; в самом деле, если R – звонкость, то / b / R / p / 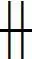/ p / R / b /, поскольку только / b / находится в отношении звонкости к / p /, а / p / находится в отношении глухости к / b /.