Александр Ивин - Логика

Очевидно, что хотя импликация полезна для многих целей, она не совсем согласуется с обычным пониманием условной связи. Импликация охватывает многие важные черты «логического поведения» условного высказывания, но вместе с тем не является достаточно адекватным его описанием.

В последние полвека были предприняты энергичные попытки реформировать теорию импликации. При этом речь шла не об отказе от описанного понятия импликации, а о введении, наряду с ним, другого понятия, учитывающего не только истинностные значения высказываний, но и связь их по содержанию.

С импликацией тесно связана эквивалентность , называемая иногда «двойной импликацией».

Эквивалентность – сложное высказывание « A , если и только если B », образованное из высказываний A и B и разлагающееся на две импликации: «если A , то B » и «если B , то A ». Например: «Треугольник является равносторонним, если и только если он является равноугольным». Термином «эквивалентность» обозначается и связка «…, если и только если …», с помощью которой из двух высказываний образуется данное сложное высказывание. Вместо «…, если и только если …» для этой цели могут использоваться «… в том и только том случае, когда…», «… тогда и только тогда, когда…» и т.п.

Если логические связки определяются в терминах истины и лжи, эквивалентность истинна тогда и только тогда, когда оба составляющие её высказывания имеют одно и то же истинностное значение , т.е. когда они оба истинны или оба ложны. Соответственно, эквивалентность является ложной, когда одно из входящих в неё высказываний истинно, а другое ложно.

Обозначим эквивалентность символом ↔, формула A ↔ B может быть прочитана так: « A , если и только если B ». Таблица истинности для эквивалентности приводится.

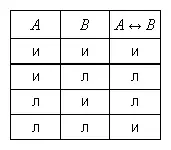
С использованием введённой логической символики связь эквивалентности и импликации можно представить так: « A ↔ B » означает « (А → В) & (В → А) ».

Например: высказывание «Ромб является квадратом, если и только если все углы ромба прямые» означает «Если ромб есть квадрат, то все углы ромба прямые, и если все углы ромба прямые, то ромб есть квадрат».

Эквивалентность является отношением типа равенства. Как и всякое такое отношение, эквивалентность высказываний является рефлексивной(всякое высказывание эквивалентно самому себе), симметричной(если одно высказывание эквивалентно другому, то второе эквивалентно первому) и транзитивной(если одно высказывание эквивалентно другому, а другое – третьему, то первое высказывание эквивалентно третьему).

В следующей таблице перечислены все шесть связок, которые были введены ранее:

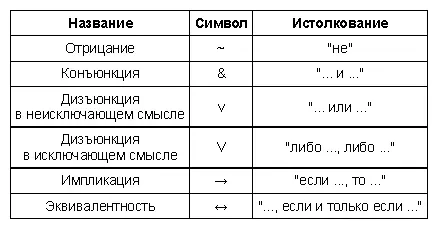
Следующие примеры показывают употребление данных связок.

Эти таблицы показывают, что формулы (А → A), (A v ~ A) , ~ (A & ~ А), ((А → В) & А) → B и ((A → В) & ~ В) → ~ A принимают значение истинно при любых значениях входящих в них переменных. Такие формулы называются общезначимыми , или тождественно истинными , или тавтологиями . Более подробно об общезначимых формулах, представляющих законы логики, говорится в главе, посвящённой этим законам.

И в обычном языке, и в логике употребляется несколько видов высказываний. До сих пор речь шла только об одном из них – об описательных высказываниях. Главной функцией описательного высказывания является описание действительности.Если высказывание описывает реальное положение дел, оно считается истинным, если не соответствует реальности – ложным. Обычно само понятие описательного высказывания определяют в терминах истины и лжи: высказывание есть повествовательное предложение, рассматриваемое вместе с его содержанием (смыслом) как истинное или ложное.

Описательное высказывание чаще всего имеет грамматическую форму повествовательного предложения: «Плутоний – химический элемент», «У ромба четыре стороны» и т.п. Однако описание может выражаться и предложениями других видов; даже вопросительное предложение способно в подходящем контексте выражать описание. Описательное высказывание отличается от высказываний иных видов не грамматической формой, а прежде всего своей основной функцией и особенностями составляющих его структурных «частей».

Описательное отношение высказывания к действительности иногда отмечается словами «истинно», «действительно» и т.п., но чаще всего никак не обозначается. Сказать «Трава зелёная» все равно, что сказать «Истинно, что трава зелёная» или «Трава действительно зелёная».

Всякое описание предполагает следующие четыре части, или компонента: субъект– отдельное лицо или сообщество, дающее описание; предмет– описываемая ситуация; основание– точка зрения, с которой производится описание, и характер– указание истинности или ложности предлагаемого описания. Не все эти части находят явное выражение в каждом описательном высказывании. Характер высказывания, как правило, не указывается: оборот «истинно, что…» опускается, вместо высказываний с оборотом «ложно, что…» используются отрицательные высказывания. Предполагается, что основания всех описательных высказываний совпадают: если оцениваться объекты могут с разных позиций, то описываются они всегда с одной и той же точки зрения. Предполагается также, что какому бы субъекту ни принадлежало описание, оно остаётся одним и тем же. Отождествление оснований и субъектов описаний составляет основное содержание идеи интерсубъективности знания – независимости его употребления и понимания от лиц и обстоятельств. Требование совпадения субъектов и оснований описаний предписывает исключать упоминание этих двух частей из состава описания. Вместо того, чтобы говорить «Для каждого человека с любой точки зрения истинно, что Земля вращается вокруг Солнца», мы говорим «Земля вращается вокруг Солнца».

К описательным высказываниям близки так называемые неопределённыевысказывания типа: «Этот дом голубой», «Здесь растёт дерево», «Завтра будет солнечное затмение» и т.п. Такие высказывания, взятые сами по себе, не являются ни истинными, ни ложными, они приобретают истинностное значение только в конкретной ситуации, в частности, в результате указания пространственно-временных координат.