Александр Ивин - Логика

( ~ B → ~ А) → (А → В) ,

если дело обстоит так, что если не- B , то не- A , то если A , то В .

К примеру: из высказывания «Если есть следствие, то есть и причина» следует высказывание «Если нет причины, нет и следствия», и из второго высказывания вытекает первое.

К законам контрапозиции обычно относят также законы:

(А → ~ В) → (В → ~ А) ,

если дело обстоит так, что если A , то не- B , то если B , то не- A Например, «Если квадрат не является треугольником, то треугольник не квадрат»;

(~ А → В) → (~ В → А) ,

если верно, что если не- A , то B , то если не- B то A . К примеру: «Если не являющееся очевидным сомнительно, то не являющееся сомнительным очевидно».

Контрапозиция подобна рокировке в шахматной игре. И подобно тому, как редкая партия проходит без рокировки, так и редкое наше рассуждение обходится без контрапозиции.

Слово «модус» в логике означает разновидность некоторой общей формы рассуждения. «Модус поненс» – термин средневековой логики, обозначающий определённое правило вывода и соответствующий ему логический закон.

Правило вывода модус поненс, обычно называемое правилом отделения или гипотетическим силлогизмом , позволяет от утверждения условного высказывания и утверждения его основания (антецедента) перейти к утверждению следствия (консеквента) этого

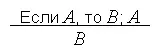
Здесь «если A , то B » и « A » – посылки, « B » – заключение; горизонтальная черта стоит вместо слова «следовательно». Другая запись:

Если A , то B. А . Следовательно, В .

Благодаря этому правилу от посылки «если A , то B », используя посылку « A », мы как бы отделяем заключение « B ». Например:

Если у человека грипп, он болен.

У человека грипп.

Человек болен.

Это правило постоянно используется в наших рассуждениях. Впервые оно было сформулировано, насколько можно судить, учеником Аристотеля Теофрастом ещё в III в. до н.э.

Соответствующий правилу отделения логический закон формулируется так:

(А → В) & A → B ,

если верно, что если A , то B , и A , то верно B . Например: «Если при дожде трава растёт быстрее и идёт дождь, то трава растёт быстрее».

Рассуждение по правилу модус понёс идёт от утверждения основания истинного условного высказывания к утверждению его следствия. Это логически корректное движение мысли иногда путается со сходным, но логически неправильным её движением от утверждения следствия истинного условного высказывания к утверждению его основания.

Например, правильным является умозаключение:

Если висмут – металл, он проводит электрический ток.

Висмут – металл.

Висмут проводит электрический ток.

Но внешне сходное с ним умозаключение:

Если висмут – металл, он проводит электрический ток.

Висмут проводит электрический ток.

Висмут металл.

логически некорректно. Рассуждая по последней схеме, можно от истинных посылок прийти к ложному заключению. Например:

Если человек собирает марки, он коллекционер.

Человек – коллекционер.

Человек собирает марки.

Далеко не все коллекционеры собирают именно марки; из того, что человек коллекционер, нельзя заключать, что он собирает как раз марки. Истинность посылок не гарантирует истинности заключения.

Против смешения правила модус поненс с указанной неправильной схемой предостерегает совет: от подтверждения основания к подтверждению следствия заключать можно, от подтверждения следствия к подтверждению основания – нет.

Так средневековые логики называли следующую схему рассуждения:

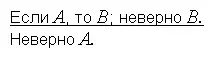
Другая запись:

Если A , то B . Не- B . Следовательно, не- A .

Эта схема часто называется принципом фальсификации : если из какого-то утверждения вытекает следствие, оказывающееся ложным, это означает, что и само утверждение ложно. Посредством схемы от утверждения условного высказывания и отрицания его следствия осуществляется переход к отрицанию основания данного высказывания. Например:

Если гелий – металл, он электропроводен.

Гелий неэлектропроводен.

Гелий – не металл.

Этим именем средневековые логики обозначали следующие схемы рассуждения:

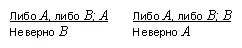
Другая запись:

Либо A , либо В. А . Следовательно, не- B .

Либо A , либо В. В . Следовательно, не- А .

Посредством этих схем от утверждения двух взаимоисключающих альтернатив и установления того, какая из них имеет место, осуществляется переход к отрицанию второй альтернативы: либо первое, либо второе, но не оба вместе; есть первое; значит, нет второго. Например:

Достоевский родился либо в Москве, либо в Петербурге.

Он родился в Москве.

Неверно, что Достоевский родился в Петербурге.

Дизъюнкция, входящая в данную схему, является исключающей, она означает: истинно первое или истинно второе, но не оба вместе. Такое же рассуждение, но с неисключающей дизъюнкцией (первое или второе, но возможно, что и первое, и второе), логически неправильно. От истинных посылок оно может вести к ложному заключению:

На Южном полюсе был Амундсен или был Скотт.

На Южном полюсе был Амундсен.

Неверно, что там был Скотт.

Обе посылки истинны: и Амундсен, и Скотт достигли Южного полюса, заключение же ложно, Правильным является умозаключение:

На Южном полюсе первым был Амундсен или Скотт.

На этом полюсе первым был Амундсен.

Неверно, что там первым был Скотт.

Этим термином средневековые логики обозначали разделительно-категорическое умозаключение : первое или второе; не первое; значит, второе. Первая посылка умозаключения – разделительное (дизъюнктивное) высказывание, вторая – категорическое высказывание, отрицающее один из членов дизъюнкции; заключением является другой её член:

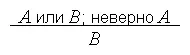
Или:

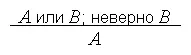
Другая форма записи:

A или B . Не- A Следовательно, В .

A или B . Не- B . Следовательно, А .

Например: