Александр Ивин - Логика

Множество является конечным или оно бесконечно.

Множество не является конечным.

Множество бесконечно.

Иногда эту схему рассуждения именуют дизъюнктивным силлогизмом .

С использованием логической символики умозаключение формулируется так:

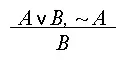
Или:

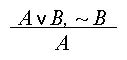
В современной логике модус толлендо поненс называется также правилом удаления дизъюнкции . Ему соответствует логический закон:

(A v B) & ~ A → B ,

если A или B и ~ A , то В .

Широкое применение находят законы, названные именем американского логика А. де Моргана и позволяющие переходить от утверждений с союзом «и» к утверждениям с союзом «или», и наоборот:

~ (A & B) → (~ A v ~ В) ,

если неверно, что есть и первое, и второе, то неверно, что есть первое, или неверно, что есть второе;

( ~ A v ~ В) → ~ (А & В) ,

если неверно, что есть первое, или неверно, что есть второе, то неверно, что есть первое и второе. Используя эти законы, от высказывания «Неверно, что изучение логики и трудно, и бесполезно» можно перейти к высказыванию «Изучение логики не является трудным, или же оно не бесполезно». Объединение этих двух законов даёт закон (↔ – эквивалентность, «если и только если»):

~(A & B) ↔ (~ A v ~ B) .

Словами обычного языка этот закон можно выразить так: отрицание конъюнкции эквивалентно дизъюнкции отрицаний.Например: «Неверно, что завтра будет холодно и завтра будет дождливо, тогда и только тогда, когда завтра не будет холодно или завтра не будет дождливо».

Ещё один закон де Моргана утверждает, что отрицание дизъюнкции эквивалентно конъюнкции отрицаний:

~ (A v В) ↔ ( ~ А & ~ В) ,

неверно, что есть первое или есть второе, если и только если неверно, что есть первое, и неверно, что есть второе. Например: «Неверно, что ученик знает арифметику или знает геометрию, тогда и только тогда, когда он не знает ни арифметики, ни геометрии». На основе законов де Моргана связку «и» можно определить, используя отрицание, через «или», и наоборот:

– « A и B » означает «неверно, что не- A или не- B »,

– « A или B » означает «неверно, что не- A и не -В ».

К примеру: «Идёт дождь и идёт снег» означает «Неверно, что нет дождя или нет снега»; «Сегодня холодно или сыро» означает «Неверно, что сегодня не холодно и не сыро».

Редукция к абсурду(приведение к нелепости) – это рассуждение, показывающее ошибочность какого-то положения путём выведения из него абсурда, т.е. логического противоречия.Если из высказывания A выводится как высказывание B , так и его отрицание, то верным является отрицание A . Например, из высказывания «Треугольник – это окружность» вытекает с одной стороны то, что треугольник имеет углы (быть треугольником значит иметь три угла), с другой, что у него нет углов (поскольку он окружность); следовательно, верным является не исходное высказывание, а его отрицание «Треугольник не является окружностью».

Закон приведения к абсурду представляется формулой:

(А → В) & (А → ~ В) → ~ A ,

если (если A , то В) и (если A , то не- B ), то не- A

Приведение к нелепости, замечает математик Д. Пойа, имеет некоторое сходство с иронией, любимым приёмом сатирика: ирония принимает определённую точку зрения, подчёркивает её и затем настолько её утрирует, что в конце концов приводит к явному абсурду.

Частный закон приведения к абсурду представляется формулой:

(А → ~ А) → ~ А ,

если (если A , то не- A ), то не -А . Например, из положения «Всякое правило имеет исключения», которое само является правилом, вытекает высказывание «Есть правила, не имеющие исключений»; значит, последнее высказывание истинно.

Закон косвенного доказательства позволяет заключить об истинности какого-то высказывания на основании того, что отрицание этого высказывания влечёт противоречие.Например: «Если из того, что 17 не является простым числом, вытекает как то, что оно делится на число, отличное от самого себя и единицы, так и то, что оно не делится на такое число, то 17 есть простое число».

Символически закон косвенного доказательства записывается так:

(~ А → В) & (~ А → ~ В) → A ,

если (если не- A , то В) и (если не- A , то не- В) , то А .

Законом косвенного доказательства обычно называется и формула:

(~ А → (В & ~ В)) → A ,

если (если не -А , то B и не- B) , то A . К примеру: «Если из того, что 10 не является чётным числом, вытекает, что оно делится и не делится на 2, то 10 – чётное число».

Закон Клавияхарактеризует связь импликации и отрицания. Он читается так: если из отрицания некоторого высказывания вытекает само это высказывание, то оно является истинным.Или, короче: высказывание, вытекающее из своего собственного отрицания, истинно.Или иначе: если необходимым условием ложности некоторого высказывания является его истинность, то это высказывание истинно. Например, если условием того, чтобы машина не работала, является её работа, то машина работает.

Закон назван именем Клавия – учёного-иезуита, жившего в XVI в., одного из изобретателей григорианского календаря. Клавий первым обратил внимание на этот закон в своём комментарии к «Геометрии» Евклида. Одну из своих теорем Евклид доказал, выведя из её допущения, что она является ложной.

Символически закон Клавия представляется формулой:

(~ А → А) → A ,

если не- A имплицирует A , то верно А .

Из закона Клавия вытекает следующий совет, касающийся доказательства: если хочешь доказать A , выводи A из допущения, что верным является не- A Например, нужно доказать утверждение «У трапеции четыре стороны». Отрицание этого утверждения: «Неверно, что у трапеции четыре стороны». Если из этого отрицания удаётся вывести само утверждение, это будет означать, что оно истинно.

Эту схему рассуждения использовал однажды древнегреческий философ Демокрит в споре с софистом Протагором. Последний утверждал, что истинно все то, что кому-либо приходит в голову. На это Демокрит ответил, что из положения «Каждое высказывание истинно» вытекает истинность и его отрицания: «Не все высказывания истинны». И значит, это отрицание, а не положение Протагора, на самом деле истинно.