Александр Ивин - Логика

По схеме первой фигуры построен силлогизм:

Все птицы (М) имеют крылья (Р) .

Все страусы (S) – птицы (М) .

Все страусы имеют крылья.

По схеме второй фигуры построен силлогизм:

Все рыбы (Р) дышат жабрами (М) .

Киты (S) не дышат жабрами (М) .

Все киты не рыбы.

По схеме третьей фигуры построен силлогизм:

Все бамбуки (М) цветут один раз в жизни (Р) .

Все бамбуки (М) – многолетние растения (S) .

Некоторые многолетние растения цветут один раз в жизни.

По схеме четвёртой фигуры построен силлогизм:

Все рыбы (Р) плавают (М) .

Все плавающие (М) живут в воде (S) .

Некоторые живущие в воде – рыбы.

Посылками и заключениями силлогизмов могут быть категорические суждения четырех видов: SaP, SiP, SeP и SoP .

Модусами силлогизма называются разновидности фигур, отличающиеся характером посылок и заключения.

Всего с точки зрения всевозможных сочетаний посылок и заключения в каждой фигуре насчитывается 64 модуса. В четырех фигурах 4 × 64 = 256 модусов.

Силлогизмы, как и все дедуктивные умозаключения, делятся на правильныеи неправильные. Задача логической теории силлогизма – систематизировать правильные силлогизмы, указать их отличительные черты.

Из всех возможных модусов силлогизма только 24 модуса являются правильными, по шесть в каждой фигуре. Вот традиционно принятые названия правильных модусов первых двух фигур:

1-я фигура: Barbara, Celarent, Darii, Ferio, Barbari, Celaront ;

2-я фигура: Cesare, Camestres, Festino, Baroco, Cesaro, Camestros .

В каждом из этих названий содержатся три гласных буквы. Они указывают, какие именно категорические высказывания используются в модусе в качестве его посылок и заключения. Так, название Celarent означает, что в этом модусе первой фигуры большей посылкой является общеотрицательное высказывание (SeP) , меньшей – общеутвердительное (SaP) и заключением – общеотрицательное высказывание (SeP) .

Из 24 правильных модусов силлогизма 5 являются ослабленными: заключениями в них являются частноутвердительные или частноотрицательные высказывания, хотя в случае других модусов эти же посылки дают общеутвердительные или общеотрицательные заключения (ср. модусы Cesare и Cesaro второй фигуры). Если отбросить ослабленные модусы, остаётся 19 правильных модусов силлогизма.

Для оценки правильности силлогизма могут использоваться круги Эйлера, иллюстрирующие отношения между объёмами имён.

Возьмём, для примера, силлогизм:

Все металлы (М) ковки (Р) .

Железо (S) – металл (М) .

Железо (S) ковко (Р).

Отношения между тремя терминами этого силлогизма (модус Barbara) представляются тремя концентрическими кругами. Эта схема интерпретируется так: если все М (металлы) входят в объём Р (ковких тел), то с необходимостью S (железо) войдёт в объём Р (ковких тел), что и утверждается в заключении «Железо ковко».

Другой пример силлогизма:

Все рыбы (Р) не имеют перьев (М) .

У всех птиц (S) есть перья (М) .

Ни одна птица (S) не является рыбой (Р) .

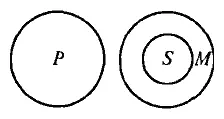
Отношения между терминами данного силлогизма (модус Cesare) представлены на рисунке. Он истолковывается так: если все S (птицы) входят в объём М (имеющие перья), а М не имеет ничего общего с Р (рыбы), то у S (птицы) нет ничего общего с Р (рыбы), что и утверждается в заключении.

Пример неправильного силлогизма:

Все тигры (М) – млекопитающие (Р) .

Все тигры (М) – хищники (S) .

Все хищники (S) – млекопитающие (Р).

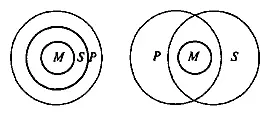
Отношения между терминами данного силлогизма могут быть представлены двояко, как это показано на рисунке. И в первом, и во втором случаях все М (тигры) входят в объём Р (млекопитающие) и все М входят также в объём S (хищники). Это соответствует информации, содержащейся в двух посылках силлогизма. Но отношение между объёмами Р и S может быть двояким. Охватывая М , объём S может полностью входить в объём Р или объём S может лишь пересекаться с объёмом Р . В первом случае можно было бы сделать общее заключение «Все хищники – млекопитающие», но во втором случае правомерно только частное заключение «Некоторые хищники – млекопитающие». Информации, позволяющей сделать выбор между этими двумя вариантами, в посылках не содержится. Значит, мы не вправе делать общее заключение. Силлогизм не является правильным.

В силлогизме, как и во всяком дедуктивном умозаключении, в заключении не может содержаться информация, отсутствующая в посылках. Заключение только развёртывает информацию посылок, но не может привносить новую информацию, отсутствующую в них.

В обычных рассуждениях нередки силлогизмы, в которых не выражается явно одна из посылок или заключение. Такие силлогизмы называются энтимемами . Примеры энтимем: «Щедрость заслуживает похвалы, как и всякая добродетель», «Он – учёный, поэтому любопытство ему не чуждо», «Керосин – жидкость, поэтому он передаёт давление во все стороны равномерно» и т.п. В первом случае опущена меньшая посылка «Щедрость – это добродетель», во втором – большая посылка «Всякому учёному не чуждо любопытство», в третьем – опять-таки большая посылка «Всякая жидкость передаёт давление во все стороны равномерно».

Для оценки правильности рассуждения в энтимеме следует восстановить её в полный силлогизм.

Об И. Ньютоне рассказывают, что, будучи студентом, он начал изучение геометрии, как было принято в то время, с чтения «Геометрии» Евклида. Знакомясь с формулировками теорем, он видел, что они справедливы, и не изучал доказательства. Его удивляло, что люди затрачивают столько усилий, чтобы доказать совершенно очевидное.

Позднее Ньютон изменил своё мнение о необходимости доказательств в математике и других науках и хвалил Евклида как раз за безупречность и строгость его доказательств.

Невозможно переоценить значение доказательств в нашей жизни и особенно в науке. И тем не менее доказательства встречаются не так часто, как хотелось бы. К доказательствам прибегают все, но редко кто задумывается над тем, что означает «доказать», почему доказательство «доказывает», всякое ли утверждение можно доказать или опровергнуть, все ли нужно доказывать и т.п.