Леонид Хренов - Время и календарь

Постоянные календари.Вследствие упомянутых недостатков григорианского календаря определение дня недели календарных дат очень затруднено, а такие определения необходимы не только при изучении истории или определении знаменательных дат, но и при археологических и литературных исследованиях и в других самых различных случаях. Например, при расчетах заработной платы, при определении числа рабочих дней в году, средней производительности Труда, при планировании пятилетних планов и других мероприятий, при определении объема продукции за некоторый отрезок времени, а также при возникновении необходимости установить день недели прошедших или предстоящих дат. Они необходимы в судебной практике и установлении дат различных мероприятий, проводимых один раз в несколько лет, например олимпиад.

Все это и явилось причиной дальнейшего развития календарных систем путем разработки постоянных («вечных») календарей, позволяющих решение перечисленных выше задач производить с меньшей затратой времени и труда.

В настоящее время известны постоянные календари самых различных устройств, составленные как на короткие, так и на длительные промежутки времени, позволяющие определять день недели любой календарной даты юлианского или григорианского календаря или сразу обоих, — универсальные календари. Все многообразие постоянных календарей можно разделить на календари аналитические — формулы различной сложности, позволяющие по заданной дате вычислять день нежели любой прошедшей и будущей календарной даты, и табличные — таблицы различной конструкции как с неподвижными, так и с подвижными частями.

Постоянные табличные календари могут быть краткосрочными (однопериодными), предназначенными лишь для одного 28-летнего периода (цикла) [51] Такой период выбран не случайно: число 28 является общим наименьшим кратным двух чисел — 4 (через четыре года повторяется високосный год) и 7 (число дней в неделе). В настоящее время в нашей стране выпускаются календари на более короткие промежутки времени — например, с 1976 по 2000 гг. ; среднесрочными (вековыми), предназначенными лишь для одного определенного периода в пределах от 28 до 100 лет; долгосрочными (постоянными), рассчитанными на значительные по продолжительности периоды от 100 и более лет.

В последние сто лет в разных странах предложены различные календарные формулы [52] См. Буткевич А. В., Зеликсон М. С. Вечные календари. — 2-е изд., перераб. и доп. — М.: Наука, 1984. ; из них первая была опубликована в России Н. И. Черухиным — (Русская старина. — 1873. — № 7). Первое же правило, позволяющее определять по заданной дате день недели, было опубликовано В. И. Штейнгелем в 1819 г. в его работе «Опыт времяисчисления» (СПб, 1819).

Поскольку все существующие календарные формулы опубликованы без их вывода, можно считать, что они были получены методом подбора. Этим и объясняется большая их разновидность. При этом многие формулы действительны только для нового стиля и не позволяют непосредственно определять день недели календарных событий, имевших место в нашей стране до 1918 г. Формулы отличаются еще и тем, что в одних за первый день недели принято воскресенье, а в других — понедельник. (Только с 1976 г. согласно стандарту Международной организации стандартов 2015–1976 за первый день недели принят понедельник.)

Большинство формул из-за своей сложности трудно запоминаются. Для некоторых требуется подсчитывать количество дней, прошедших от начала года до заданной даты, а для других — для каждого месяца определять свой коэффициент.

При выводе формулы примем следующие обозначения: К — календарное число месяца; М — коэффициент месяца; J — полный номер года н. э.; Д — порядковый номер года в столетии; Г' — сдвиг дней недели по годам; Г — коэффициент года; В — коэффициент века; С — число полных прошедших столетий; [] — целая часть частного от деления (неполное частное); | | — остаток от деления, причем если делимое меньше делителя, остаток равен делимому; d — порядковый номер дня недели (0 — воскресенье, вс; 1 — понедельник, пн; 2 — вторник, вт; 3 — среда, ср; 4 — четверг, чт; 5 — пятница, пт; 6 — суббота, сб).

День недели календарной даты определяется как остаток от деления суммы чисел К, М, Г и В на 7:

d = |( K+ M + Г + В) / 7 | (1)

Сделаем предположение, что 1 января 1 г. п. э. был понедельник (= 1). Тогда для дат января первого года день недели будет определяться по формуле

d = |К / 7 |.

Так как в январе 31 день, то день недели в феврале первого года определится по формуле

d = |(К + (31–28)) / 7 | = |(K + 3) / 7 |.

Здесь 28 — ближайшее к 31 число, кратное семи, которое мы вычитаем для упрощения вычислений.

Так как в феврале первого года 28 дней, то день недели в марте определяется так же, как и в феврале. В марте 31 день, поэтому для апреля получим формулу

d = |(К + 3 + (31–28)) / 7 | = |(K + 6) / 7 |.

Аналогично получим формулы для остальных месяцев. В этих формулах числа, прибавляемые к календарному числу К, суть коэффициенты месяцев М, которые мы свели в табл. 9.

Таким образом, день недели для первого года н. э. будет определяться по формуле

d = |(K + M) / 7 |. (2)

Объединив повторяющиеся в табл. 9 значения М для разных месяцев, получим табл. 10.

Так как в простом году 52 недели и один день (365 = 52×7 + 1), то для второго года н. э. календарная формула примет вид

d = |(K + M + 1) / 7 |.

а для третьего

d = |(К + М + 2) / 7 |.

Следующий год (четвертый) — високосный; в нем 366 дней (за счет увеличения числа дней в феврале: 29 вместо 28). Поэтому для 4 г. н. э. календарная формула принимает вид для января и февраля

d = |(K = M + 3) / 7 |.

а для месяцев с марта по декабрь

d = |(K = M + 4) / 7 |.

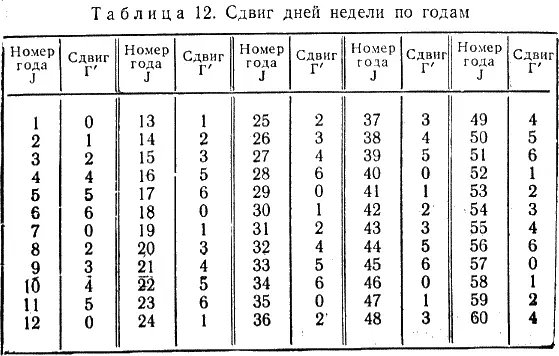
В табл. 11 приведены коэффициенты М для високосных (вис.) и невисокосных — простых (пр.) лет. Так как сдвиг дней недели по годам Г' в четырехлетиях 1–4, 5–8, 9–12 и т. д. происходит одинаково, составим таблиц значений Г' для J от 1 до 60 лет (табл. 12). Мы видим, что в каждом следующем четырехлетии значение сдвига Г' «увеличивается» на 5. Это позволяет выразить его для високосных годов (J вис) в виде формулы

Г' = |(5(Jвис:4) — 1) / 7)|

а для простых (J np ) в виде формулы