Леонид Хренов - Время и календарь

До 1956 г. значение секунды принималось равным 1:86 400 части средних солнечных суток, определяемых по вращению Земли вокруг своей оси. Для более точного определения секунды в 1960 г. XI Генеральная конференция по мерам и весам утвердила рекомендованную IX конгрессом MAC в 1955 г. ее значение как 1:315 569 25,9747 часть тропического года, каким он был на начало 1900 г. Такая секунда была названа эфемеридной ; она определяется с погрешностью до (2–5) · 10 - 9 . За начало средних солнечных суток принимают момент нижней кульминаций среднего солнца. Такой счет времени называют гражданским временем .

В СССР гражданским временем в народном хозяйстве пользуются с 1919 г., а в астрономии — с 1925 г. Часы, которыми мы пользуемся, отрегулированы не по истинному, а по среднему солнечному времени. Так как скорость среднего солнца одинакова и через меридиан оно проходит раньше или позднее истинного Солнца, то, следовательно, средние сутки могут наступать раньше или позже истинных.

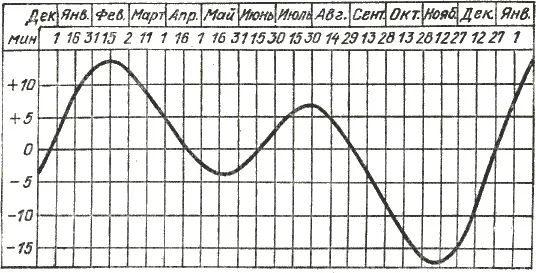
Рис. 4. График уравнения времени

Разница между истинным и средним солнечным временем η называется уравнением времени . Следовательно, в любой момент среднее солнечное время T m равно истинному солнечному времени T o плюс уравнение времени η [14] В астрономических ежегодниках приводится уравнение времени для каждого дня года. , т. е.

T m = T o + η ,

где η имеет положительное значение, когда истинное Солнце находится на эклиптике впереди среднего, и отрицательное — когда среднее солнце находится впереди истинного. (Знаком Θ в астрономии обозначается Солнце.)

На рис. 4 приведен график изменения уравнения времени в течение года через полмесяца. Уравнение времени бывает равно нулю около 15 апреля, 14 июня, 31 августа и 25 декабря, когда истинное солнечное время почти совпадает со средним солнечным; в эти дни часы, установленные по среднему солнечному времени, будут показывать в полдень 12 часов. Наибольшее (по абсолютной величине) отрицательное значение уравнения времени (см. рис. 4), η = — 16,5 минуты, бывает около 4 ноября, а наибольшее положительное, η = + 14,3 минуты, — 12 февраля.

Из определения среднего солнечного времени следует, что оно относится к тому месту, где производятся наблюдения. Следовательно, среднее солнечное время имеет свое собственное значение для каждого меридиана на Земле и поэтому его называют еще местным средним временем [15] Для облегчения отсчета местного времени в 1967 г. в английском журнале «Нью сайентист» было предложено вместо деления суток на 24 часа считать в них 10 часов, деля каждый такой час на 100 минут, а минуту — на 100 секунд. В связи с этим предложено и дугу земного экватора делить не на 360°, а на 1000 градусов; при этом выполнялись бы соотношения 1 час = 100°, 1° = 1 мин. .

Для любой точки одного и того же меридиана местное время сохраняет постоянное значение, но с изменением долготы места наблюдений меняется и местное среднее время. Когда в Москве полдень, то на противоположной стороне земного шара, т. е. на 180° к западу или к востоку от Москвы, в этот момент будет полночь. В течение одного часа небесная сфера в своем видимом движении поворачивается на 1/24 часть ее полного оборота, что в угловых единицах соответствует 360°: 24 = 15°. Поэтому два пункта на Земле, имеющие разность долгот в 15°, будут иметь местное время, отличающееся на 1 час. Если от первоначального места наблюдения передвинуться по долготе, например, на 30° (т. е. на два часа) к востоку или к западу, то в первом случае Солнце, очевидно, пройдет через меридиан нового места наблюдения на два часа раньше, а во втором случае, наоборот, на два часа позднее, чем в первоначальном пункте. Следовательно, по разности показаний часов, идущих по местному времени в разных пунктах Земли, можно судить о разности долгот этих пунктов.

В соответствии с международным соглашением (Рим, 1883 г.) за начальный меридиан для счета географических долгот на нашей планете принят Гринвичский меридиан с долготой, равной 0°00′00″, а местное гринвичское время, отсчитываемое от полуночи, условились называть всемирным или мировым временем ( T o ). Поэтому, когда в Гринвиче (около Лондона) наступает полночь, т. е. 00 ч 00 мин 00 с среднего местного времени, местное среднее время любого пункта на нашей планете будет равно долготе этого пункта, выраженной в часовой мере. Другими словами, разность долгот двух пунктов равна разности местных времен в этих пунктах в один и тот же момент. На этом и основано измерение долготы.

Наличие в различных пунктах, лежащих на разных меридианах, своего местного времени приводило ко многим неудобствам.

В 1878 г. канадский инженер С. Флеминг предложил так называемое поясное время ( Т п ), которое в 1884 г. было принято на Международном астрономическом конгрессе. По идее С. Флеминга вся поверхность земного шара условно разделяется меридианами на 24 часовых пояса протяженностью каждый в 15° (1 час) по долготе. Во всех точках каждого часового пояса устанавливается время, соответствующее среднему меридиану данного пояса.

Каждому из 24 часовых поясов присваивается соответствующий номер от 0 (нулевого) до 23-го. За нулевой принят пояс, средним меридианом которого является Гринвичский, от которого нумерация поясов ведется с запада на восток. Средний меридиан первого пояса находится к востоку от Гринвичского меридиана на 15°, или на 1 час по времени; средний меридиан второго пояса имеет восточную долготу, равную 30°, а его местное время отличается от всемирного (гринвичского) на 2 часа и т. д. Таким образом, номер каждого часового пояса показывает, на сколько целых часов время данного пояса отличается от всемирного (опережает его); при этом минуты и секунды во всех поясах остаются одинаковыми. Следовательно, поясное время при переходе из одного пояса в смежный изменяется скачком на 1 час. Если обозначить номер пояса через n , то поясное время равняется мировому T o плюс n , т. е.

T n= T o+ n.

Поясному времени некоторых часовых поясов присвоены особые названия. Так, например, время нулевого пояса называют западно-европейским, первого пояса — средне-европейским, второго пояса — восточно-европейским.

Впервые поясное время было введено в 1883 г. в Канаде и в США; в начале XX в. им стали пользоваться в некоторых европейских государствах.

В нашей стране на поясное время впервые перешли с 1 июля 1919 г. в соответствии с Декретом СНК РСФСР от 8 февраля 1918 г., и вначале им пользовались лишь для целей судоходства.