Тим Глинн-Джонс - Странности цифр и чисел.

Во время конфликта на Балканах в 1990-х годах Югославию захватила крупнейшая инфляция, вызвав многократную ревальвацию национальной валюты. В 1993 году была издана банкнота ценностью 500 000 000 000 динаров.

Основная разница между европейской и американской системой нумерации с точки зрения степени 10 в числах больше миллиона состоит в том, что в американской системе множители тысячи (10 3) вставлены между каждым именованным числом. В них используется окончание «-ард» вместо «-ион», поэтому 1 000 000 000 называется миллиардом. Однако тысяча миллиардов обычно так и называется во избежание путаницы из-за игры слов с биллиардами. Но не вся Европа использует эту систему. В Греции, Италии, России и Турции предпочитают американский миллиард.

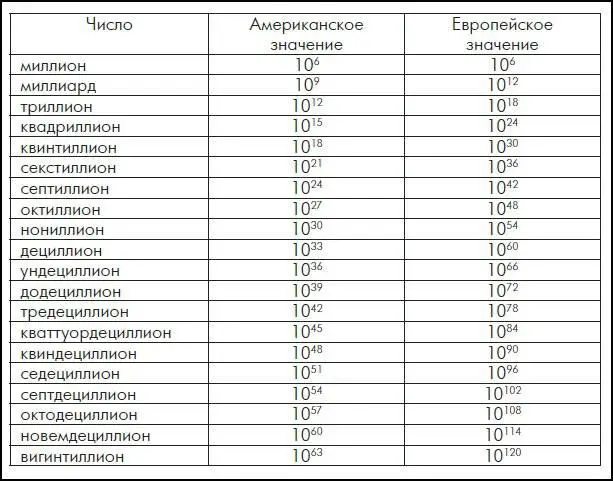
Эти названия продолжаются до центиллиона, который равен 1 0 303в США и 1 0 600в Европе. Вы можете обратить внимание, что ни в одной из этих систем нет числа для обозначения 10 100. Название этого числа появилось благодаря девятилетнему мальчику по имени Мильтон Сиротта. Он был племянником математика Эдварда Каснера, который попросил его придумать название для такого большого числа. Мильтон сказал, что у него должно быть какое-то нелепое название типа «гугол». И это название прижилось.

Поисковая система «Гугол» (Google) в Интернете была названа в честь того самого «гугола» Мильтона Си-ротты, правда с опечаткой при написании. Когда ее создатели Ларри Пэйдж и Сергей Брин проверяли, свободно ли имя этого домена, один из их студентов напечатал это название как «Google» и обнаружил, что название доступно. Это название нашло отклик в душе Пэйджа и Брина, и они оставили его.

Конечно, всегда есть что-то выше. Как же мы назовем число 10 в степени гугол? Ответ: гугол-плекс. Оно будет выглядеть как 1 с 10 100нулей. Кажется вполне закономерным, если сравнить положение нуля в начале этой книги, что он должен играть такую важную роль в образовании огромных чисел в ее конце.

Известное под названием «число Авогадро» (число молекул в 1 куб. м газа при нормальных условиях) или «постоянная Лошмидта» (число молекул, атомов, ионов и других подобных частиц в одном моле вещества). Запись 6,02 х 1 0 23отпечатывается в мозгу каждого честолюбивого студента-химика (точность числа постоянно проверяется, однако это сокращение одно из наиболее часто используемых). Эту постоянную величину открыл австрийский ученый Иоганн Йозеф Лошмидт в 1865 году, но позже число было названо в честь итальянского ученого Амедео Авогадро. Оно позволит вам рассчитать количество частиц в данном весе какой-либо субстанции на основе его атомного веса.

В 2006 году это число было открыто как самое большое известное простое число. Оно слишком длинное, и, чтобы написать его цифрами, придется потратить много бумаги. Оно состоит из 9 808 358 цифр, что на 700 000 цифр больше, чем предыдущее самое большое известное число. Его открытие являлось частью программы под названием «Обширный интернет-поиск новых простых чисел Мерсенна», которая началась в 1996 году человеком по имени Джордж Волтман. Было найдено всего лишь относительно небольшое количество простых чисел Мерсенна, не более 50, хотя программа GIMPS способствует открытию все большего количества простых чисел каждый год.

299 792 458 м/с

Скорость света

5000

Приблизительное количество звезд, видимых невооруженным глазом

13 700 000 000 лет

Предполагаемый возраст Вселенной

4,2 световых лет

Расстояние до Проксима Центавра, самой близкой к Солнцу звезды

5 879 000 000 000 миль

(9 460 730 472 580,8 км)

Световой год (расстояние, которое проходит свет в вакууме за 1 год)

1 988 500 000 000 000 000 000 000 000 000 000 г

Масса Солнца

1 000 000 000 000 000 000 000 000 000 Вт

Электрическая (активная) мощность электрического потока Солнца

5 400 000 000 000 000 000 000 000 000 г

Масса Земли

70 000 000 000 000 000 000 000

Приблизительное количество звезд во Вселенной в соответствии с исследованиями 2004 года, проводимыми д-ром Симоном Драйвером из Австралийского национального университета

93 000 000 миль (149 598 000 км)

Это 1 астрономическая единица (a.e.): расстояние от Земли до Солнца

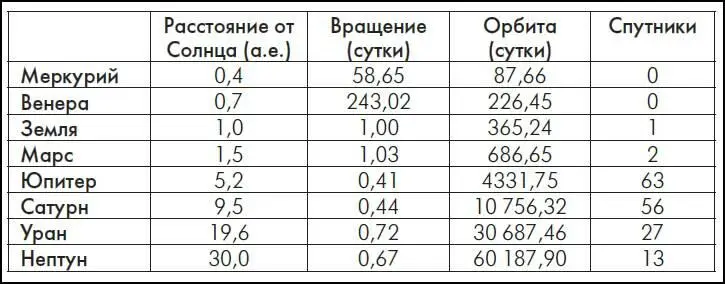
Наша Солнечная система

1 Солнце

3 карликовые планеты

8 планет

162 спутника

«Итак, ученые видят: блоха, На ней сидят блошки поменьше и сосут ее кровь,

На меньших блошках сидят еще меньшие и кусают их.

И так — до бесконечности».

Эти строки написал Джонатан Свифт, ирландский сатирик, который подарил нам «Путешествия Гулливера». В своей поэме он выражает идею, что жизнь, такая, какой мы ее знаем, повторяется в меньших и еще более меньших формах «ad infinitum» — до бесконечности. И таким же образом это может идти в другом направлении: мир, в котором мы живем, является частью внутри гигантского организма, который, в свою очередь, сам живет на частице… и так далее.

После прочтения книги о таком большом количестве чисел, каждое из которых имеет важное значение и является единицей чего-то завершенного, размышлять о бесконечности, о великом бесчисленном множестве — это вызов для человеческого мозга. Но, думая об этом, мы можем легко пропустить такие числа, как 10 гугол, так как они фактически бесполезны, кроме тех случаев, когда могут служить темой для разговора, и мы обнаруживаем, что часто нас захватывают понятия, которые требуют понимания бесконечности: Вселенная — Время — Бездна — Лента Мёбиуса — Параллельные линии — Смерть.

Одним из величайших прорывов в искусстве в эпоху Ренессанса было овладение перспективным изображением. Это достигалось нанесением точек схода — точек, в которых, как казалось, соединяются параллельные линии. Конечно, параллельные линии никогда не пересекутся. Проходя рядом, они длятся до бесконечности.

Обдумайте следующее. Объект, достигающий неподвижной точки, двигается с постоянной скоростью, по истечении 1 секунды расстояние сокращается наполовину; после 1,5 секунды расстояние снова сокращается в 2 раза; после 1,75 секунды оно снова делится пополам и так далее. По определению, объект в реальности никогда не сможет достигнуть неподвижной точки, потому что с каждой долей секунды оставшееся расстояние только сокращается в 2 раза. Как время, так и расстояние теоретически могут делиться бесконечно.