Вернер Гильде - Зеркальный мир

Одно дополнительное замечание. Вы можете встретить в учебниках такие обозначения: (100) - для кубических и (111) - для октаэдрических граней. Если даже отыскать в справочнике эти числа («индексы Миллера»), то запомнить, что они означают, не так-то просто. Рекомендуем заметить себе: грань куба пересекает одну из трех осей прямоугольной системы координат (1), а обе другие не пересекает (00). Грань октаэдра пересекает все три оси (111).

ОСНОВНЫЕ ПОСТРОЕНИЯ, ОСНОВАННЫЕ НА СИММЕТРИИ

Как разделить отрезок пополам.

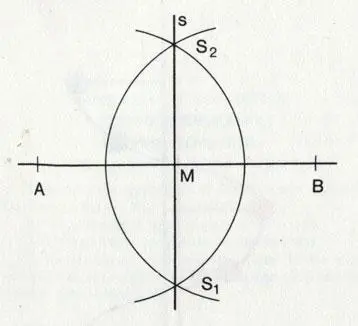
Как разделить отрезок пополам

Как разделить угол пополам.

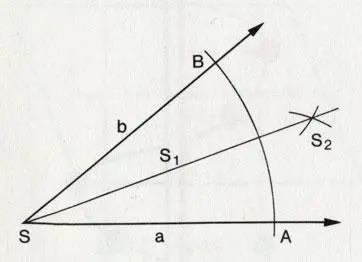
Как разделить угол пополам

Как восстановить перпендикуляр в заданной точке.

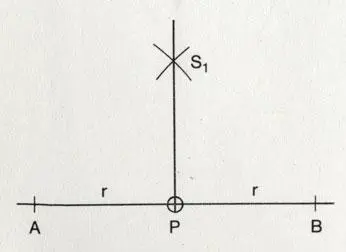
Как восстановить перпендикуляр в заданной точке

Как опустить перпендикуляр из задней точки.

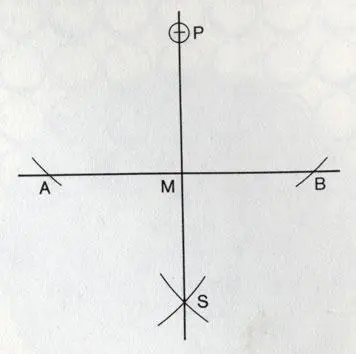
Как опустить перпендикуляр из задней точки

Как провести параллельную прямую.

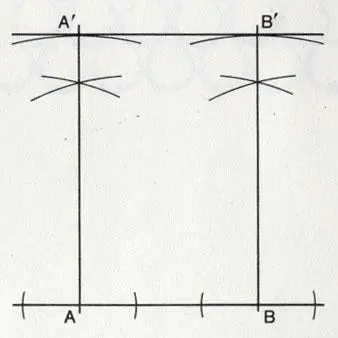
Как провести параллельную прямую

МАТЕМАТИКА ДЛЯ ПРОДАВЦОВ ФРУКТОВ

Яблоки, апельсины, грейпфруты, лимоны - излюбленные декоративные элементы оформления витрин. Для привлечения покупателей из них обычно выкладывают красочные плоские фигуры или пирамиды. Для выкладки плоских фигур могут использоваться и более мягкие фрукты и овощи - такие, как персики или помидоры.

В самом простом случае продавец фруктов или овощей ставит в витрину ящик с помидорами или персиками. Оценим наметанным глазом, соотносятся ли длины сторон ящика как 1: √ 2. «Фруктовый товар» прибывает из самых различных стран, поэтому ящики неодинаковы по величине. И все же вид этих ящиков тем привлекательнее, чем ближе их пропорции к идеальному соотношению.

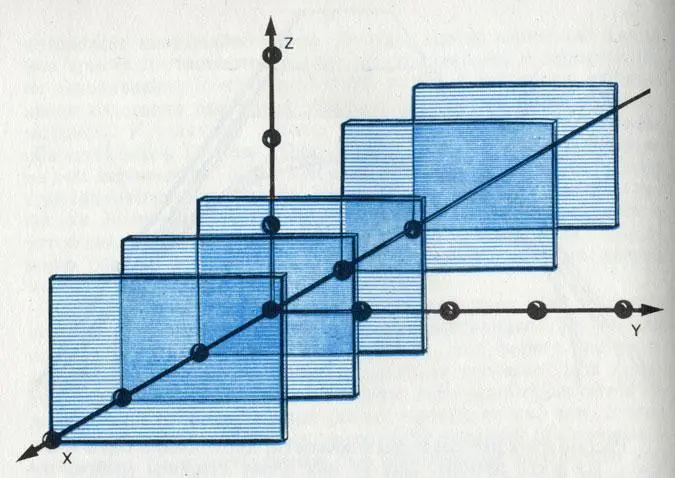
В пределах одной прямоугольной системы координат грани всегда остаются одинаковыми, на какое бы расстояние их не перемещали параллельно самим себе

Затем нас будет интересовать степень использования объема при упаковке. Цитрусовые поступают обычно с Балкан, из Африки или из других отдаленных южных краев. Перевозка их всегда стоит дорого. Поэтому фрукты должны быть упакованы не только хорошо (во избежание потерь), но и рационально, компактно (для сокращения транспортных расходов, чтобы не возрастали цены).

Возьмем ящики с помидорами. Простоты ради допустим, что все они имеют одинаково красивую форму и равную величину. Сделаем еще одно допущение - что стороны ящика имеют длину, кратную диаметру помидора. Потом возьмем и упакуем шары-помидоры так, чтобы они красиво улеглись в аккуратные прямые ряды, соприкасаясь между собой боками. В сущности говоря, упакованный подобным образом ящик сплошь состоит из квадратов, в которые вписаны круги. Площадь квадрата составляет 1Х1 = 1, если в качестве масштаба выбрать диаметр помидора. Площадь проекции помидора, напротив, равна лишь π • 0,5 2= 0,785. Соответственно площадь ящика использована для укладки помидоров только на 78,5%.

При укладке ровными прямыми рядами диски или шары заполняют площадь на 78,5%

Однако на деле фрукты и овощи круглой формы бывают уложены иначе - не в прямые ряды, а в пустые гнезда. Первый ряд вдоль длинной стороны ящика касается этой стороны и прилегает к обеим ограничивающим его коротким сторонам. Пока все обстоит так же, как и в первом случае. Но второй ряд уложен в гнезда. Выигрыш очевиден и состоит в том, что помидоры теперь несколько сдвинулись кверху. Проигрыш заключается в появлении двух пустот справа и слева в конце ряда. Третий ряд, хотя и уложен тоже в гнезда второго, но представляет собой точное зеркальное отражение первого. Четвертый ряд снова отвечает второму и т. д. При укладке последнего ряда могут встретиться два случая: либо он окажется типа ряда 1, либо типа ряда 2. Во втором случае в ящик поместится на две половинки помидора меньше, чем в первом.

При плоской укладке в пустые гнезда диски или шары заполняют площадь на 90,6%

Возьмем фрагмент укладки из середины ящика. Приглядевшись, можно увидеть, что вокруг каждого кружка (помидора) располагаются шесть других кружков. Отдельные помидоры уже не вписываются в квадрат, вершина которого соприкасается с вершинами других (мысленных) квадратов, но никак не с помидорами. И четыре помидора вместе тоже не образуют квадрата: в наименьшую структурную единицу этой укладки входит всякий раз по 1/6 площади каждого из трех кругов, окружающих маленький участок свободной поверхности. Сопоставив их размеры, найдем, что степень использования площади при такой укладке возрастает до 90,6%. Это плотнейшая из известных нам плоских укладок шаров или дисков. Иначе говоря, мы не можем разместить на плоскости шары, помидоры или монеты одного достоинства (то есть размера), не оставив незанятой ее часть, равную 9,4% всей площади. Тем не менее расположение в гнездах с использованием площади в 90,6% - большое достижение по сравнению с укладкой ровными одинаковыми рядами, где этот показатель составляет лишь 78,5%.

В торговых залах больших магазинов кассы обычно устанавливаются одна за другой в длинный ряд. В случае если они больше не в состоянии совладать с натиском покупателей, их располагают «лесенкой», так удается вместить еще одну или две кассы при той же ширине зала. Станки в токарных цехах в большинстве своем сразу устанавливаются в «промежутках», чтобы возможно лучше использовать рабочую площадь.

Обычно в днище теплообменника стремятся вварить как можно больше труб, поэтому стараются расположить их наиболее рационально - в шахматном порядке: трубы верхнего ряда над промежутками между трубами нижнего ряда