Мартин Гарднер - Есть идея!

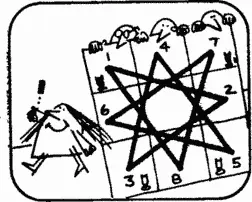
Прежде чем приступить к объяснению, Фанни начертила диаграмму, на которой отрезками прямых изображены возможные ходы каждого коня.

Мисс Фиш. Представьте себе, что отрезки прямых — это нити, а восемь клеток нанизаны на них, как бусины, и их можно расположить по окружности.

Мисс Фиш. Каждый ход на доске соответствует вполне определенному ходу на окружности. Чтобы поменять позиции коней, их необходимо переместить по окружности, двигая в одном направлении.

Мистер Бишоп. Вы совершенно правы, Фанни. Чтобы перейти на новую позицию, каждый из 4 коней должен совершить по 4 хода. Таким образом, задачу можно решить за 16 ходов, а более экономного решения не существует.

Фанни заменила одного из белых коней красным и задала членам шахматного клуба новую задачку: как поменять местами белого и красного коня за наименьшее число ходов?

Как, по-вашему, почему Фанни улыбалась, предлагая эту задачку?

Фанни решила шахматную задачу, сведя ее к изоморфной задаче, допускавшей простое (хотя и далеко не тривиальное!) решение. Поставленную Фанни задачу можно решить тем же методом. Соединив нитями клетки, занятые конями, и развернув получившееся «ожерелье» в окружность, мы увидим, что кони нанизаны на нити в следующем порядке: черный, черный, красный, белый. Фанни улыбалась, так как понимала, что переставить красного и белого коней невозможно: они следуют друг за другом в неизменном порядке, потому что ни один конь не может перепрыгнуть через другого коня, если они оба движутся по кругу (в любом направлении) и обгон запрещен. Понятно ли вам почему?

При движении по окружности по часовой стрелке белый конь всегда следует непосредственно за красным. Если бы белый и красный кони могли поменяться полями, которые они занимали на доске с самого начала, то порядок следования был бы изменен на обратный и красный конь двигался бы по кругу непосредственно за белым. Ясно, что такое перестроение невозможно. Действительно, оно означало бы, что один из коней (либо белый, либо красный) перепрыгнул через двух черных коней. Сведя мини-шахматную задачу к топологической задаче о расположении четырех точек на простой замкнутой кривой, мы получили возможность весьма просто доказать, что решения исходной задачи не существует. Получить доказательство «несуществования» другим способом было бы чрезвычайно трудно. Попробуйте, и вы убедитесь в этом сами.

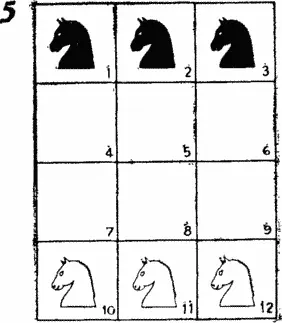
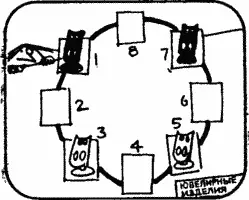
Вам понравилась задача о перестановке шахматных коней? Вот еще одна такая задача, по трудности даже превосходящая обе предыдущие. Рассмотрим позицию на шахматной доске 3×4, изображенную на рис. 5 . Как и прежде, трех черных и трех белых коней требуется поменять местами так, чтобы белые кони оказались на верхней горизонтали, а черные заняли нижнюю горизонталь, причем выполнить перестановку за наименьшее число ходов.

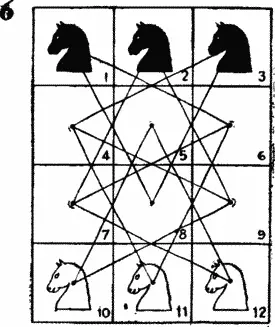
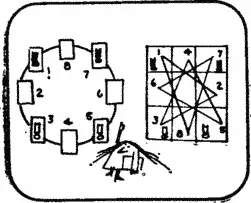
В этом случае, как видно на рис. 6 , изоморфный граф более сложен. Этот граф представляет собой диаграмму, на которой показаны все возможные ходы коней, Предположив, что вершины нашего графа — пуговицы или бусины, а ребра — нити, мы обнаружим, что развернуть его в окружность, как в предыдущей задаче, невозможно, но наш граф из нитей и пуговиц нам удастся уложить так, как показано на рис. 7 . Числа на этом рисунке соответствуют номерам клеток на рис. 4 и 5 .

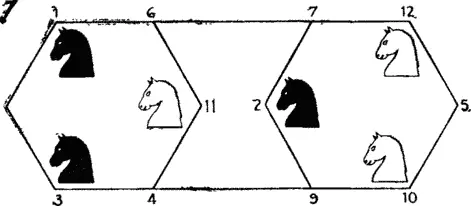
Ясно, что задача о перестановке шахматных коней на этом графе изоморфна исходной задаче, но решается несравненно легче. Удастся ли вам найти минимальное решение в 18 ходов?

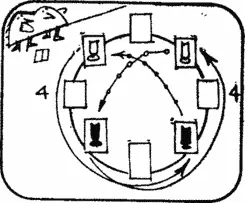
Метод нитей и пуговиц позволяет проанализировать одну старинную игру. Для нее нам понадобится особая «доска» — звездчатый граф, изображенный на рис. 8 , и семь монет или небольших фишек.

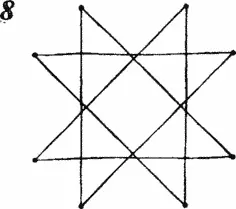
Игра состоит в следующем. Положив монету на любую вершину графа, вы можете сдвинуть ее вдоль черной ломаной линии (ребер графа) в любую другую вершину. После того как ход закончен, прикасаться к монете и перемещать ее в другую вершину запрещается.

Затем вы кладете вторую монету на любую незанятую вершину графа и передвигаете ее вдоль ребер в любую другую незанятую вершину. Так вы продолжаете действовать до тех пор, пока все семь монет не займут свое место на вершинах графа.

Очень скоро вы обнаружите, что расставить все семь монет удается, если действовать по тщательно продуманному плану: малейшая небрежность приводит к позиции, не позволяющей достичь в игре успеха. Не могли бы вы указать, каких правил следует придерживаться при расстановке и перемещении монет, чтобы вам неизменно сопутствовал успех?

Звездчатый граф можно полностью «раскрыть» подобно графам в двух первых задачах о перестановке шахматных коней, его удается развернуть в окружность. После того как это сделано, семь монет нетрудно расположить на окружности и проанализировать, как они могут двигаться. Справиться с этой задачей можно многими способами. Одна из наиболее простых выигрышных стратегий состоит в том, чтобы делать любой ход первой монетой, а все следующие монеты ставить и передвигать всегда так, чтобы по окончании хода они заняли вершину, которую занимала в исходном положении предыдущая монета.

Предложите сыграть в эту игру своим друзьям. Лишь очень немногие из них смогут расставить все семь монет, даже если вы один раз быстро продемонстрируете им, как следует играть.

Присмотритесь повнимательнее к этой картинке. Что художник нарисовал неправильно?