Виктор Звонников - Контроль качества обучения при аттестации: компетентностный подход

Для исходной матрицы данных подсчитанная ранее исправленная дисперсия S X 2 = 6,89 , а доли правильных ответов получаются делением чисел R j в последней строке матрицы на 10. Тогда сумма произведений долей правильных и неправильных ответов будет 0,9 · 0,1 + 0,8 · 0,2 + 0,7 · 0,3 + 0,6 · 0,4 + 0,5 · 0,5+ 0,5 · 0,5 + 0,3 · 0,7 + 0,4 · 0,6 + 0,2 · 0,8 + 0,1 · 0,9 = 1,9 и коэффициент надежности

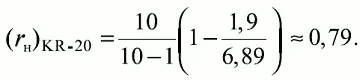
При оценке надежности нельзя полагаться лишь на один показатель, поскольку каждый из них имеет свои ограничения, смещающие оценки надежности теста в сторону завышения или занижения. Для достоверной проверки качества теста следует учитывать несколько показателей надежности, подсчитанных по разным формулам, лишь небольшая часть которых приведена в данном тексте. В качестве нижнего предела допустимых значений надежности обычно выбирают 0,7. При более низком значении использование теста вряд ли целесообразно в силу большой погрешности измерения.

Если тест разрабатывают профессионалы, то к нему предъявляют более жесткие требования. Как правило, тесты с надежностью менее 0,8 считаются непригодными в профессионально организованных службах и центрах тестирования. Значения коэффициента надежности, превышающие 0,9, говорят о высоком качестве теста. Они крайне желательны, но редко встречаются. Обычно в тестологической практике надежность тестов колеблется в интервале (0,8; 0,9). Коэффициент надежности, подсчитываемый по матрице тестовых результатов, всегда зависит от свойств выборки испытуемых. Поэтому при каждом очередном использовании теста приходится оценивать его надежность, а уж потом говорить о возможности интерпретации результатов выполнения теста.

Один из аспектов применения коэффициента надежности связан с определением стандартной ошибки измерения. Для установления связи между стандартной ошибкой измерения и надежностью теста необходимо преобразовать формулу

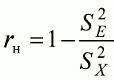
и выделить в левой части S Е 2 . После преобразования формулы относительно S Е 2 получится выражение S Е 2 = S X 2 (1 – r н) , или

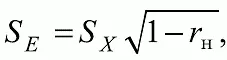
где S X — стандартное отклонение по распределению индивидуальных баллов; r н– коэффициент надежности теста; S E — стандартная ошибка измерения. Это выражение обычно используется для вычисления S E по известным величинам r ни S X Что касается сущностного смысла, то S E (standard error of measurement) трактуется как стандартное отклонение результатов испытуемого от его истинного балла, полученное при выполнении им большого числа параллельных форм теста.

Для лучшего уяснения смысла показателя S E можно представить другую гипотетическую ситуацию, когда i -и испытуемый выполнял много раз один и тот же тест. Если предположить, что эффект запоминания отсутствует, то результаты тестирования образуют нормальное распределение вокруг истинного балла Т i со стандартным отклонением S E . На практике S E рассматривается как статистическая величина, отражающая степень точности отдельных измерений, поэтому величину S E используют для определения границ доверительного интервала, внутри которого должен находиться истинный балл оцениваемого ученика группы.

Построение доверительного интервала. Общераспространен подход, когда доверительный интервал выстраивается как две симметричные окрестности (левая и правая) вокруг наблюдаемого показателя ученика, хотя это не совсем верно, поскольку речь должна идти об окрестностях, расположенных слева и справа от истинного балла. Тем не менее этот факт вынуждено игнорируется в прикладных исследованиях в силу отсутствия истинного балла, и доверительный интервал при заданном риске допустить ошибку t =̣ 0,05, т.е. в пяти случаях из ста, принимается равным ( X i – 1,96 S E ; X i + 1,96 S E ) , где Χ i — наблюдаемый балл i -го испытуемого; 1,96 – константа, табличное число, используемое при t ≤ 0,05.

Для рассматриваемого ранее примера матрицы тестовых результатов (см. табл. 6.11), коэффициента надежности r н=̣ 0,78 и стандартного отклонения S X =̣ 2,62, вычисленного ранее для матрицы, S E будет равно

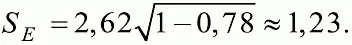
Тогда доверительный интервал для истинного балла первого ученика со значением Х i = 6 будет (6 – 1,23; 6 + 1,23) или (4,77; 7,23). Истинный балл первого ученика может находиться в любой точке этого интервала.

Интересна геометрическая интерпретация доверительного интервала на оси наблюдаемых баллов, приведенная для балла i -го учащегося. Очевидно, что с ростом S E границы доверительного интервала будут раздвигаться, и вместе с тем будут увеличиваться возможные пределы отклонения истинного балла от наблюдаемых результатов измерения (более правильная с точки зрения теории трактовка: пределы отклонения наблюдаемых баллов от истинной компоненты измерения).

Валидность – это характеристика способности теста служить поставленной цели измерения. Как правило, постановка целей создания теста носит комплексный характер, поэтому часто стараются проверить валидность с разных позиций сообразно различным направлениям использования теста. Например, нормативно-ориентированный тест для приема абитуриентов в вузы должен служить цели дифференциации испытуемых и прогностическим целям, так как мало выделить лучших абитуриентов в момент приема, нужно также спрогнозировать успешность дальнейшего обучения зачисленных в вузы абитуриентов.

Оценивание валидности всегда проводится путем соотнесения характеристик результатов измерения с внешними критериями [ 1,28, 36]. В качестве таких критериев могут выступать оценки экспертов при анализе содержания теста и его адекватности целям измерения (содержательная валидность), результатов по другим тестам (конструктная валидность), успешности дальнейшего обучения (прогностическая валидность). Высокая корреляция между анализируемыми результатами испытуемых и внешними критериями подтверждает высокую валидность теста. Основная трудность при такой валидизации носит не практический, а методологический характер, поскольку она состоит в выборе значимого внешнего критерия.