Надежда Ефремова - Тестовый контроль в образовании

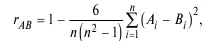
где n – число случаев; A i− B i – разность между индивидуальными рангами по х и у.

12. Стандартная ошибка измерения:

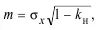
гдеσ x– стандартное отклонение; к н – коэффициент надежности.

13. Точечно–бисериальный коэффициент корреляции:

14. Коэффициент корреляции Пирсона тестовых заданий с номерами i и j :

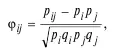
где p ij – доля тестируемых, вытолнивших верно i – е и j – е задания; p i – доля тестируемых, выполнивших верно i – е задание, q i = 1— p i ; p j– доля тестируемых, выполнивших верно j–е задание, q j = 1 – p j.

15. Коэффициент надежности:

а) коэффициент Спирмена—Брауна (метод расщепления):

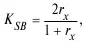
где r x – коэффициент корреляции двух частей теста;

б) коэффициент Рюлона:

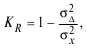
где σ 2 ∆ – дисперсия разностей результатов по каждой из двух частей теста; σ 2 x – дисперсия результатов теста;

в) коэффициент Кронбаха:

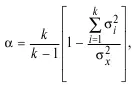
где к – количество заданий; σ 2 i– дисперсия результатов отдельных заданий; σ 2 x– дисперсия результатов теста.

г) коэффициент Кьюдера—Ричардсона:

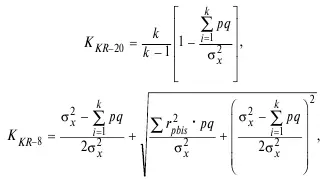
где к – количество заданий; σ 2 x: – дисперсия результатов теста; pq – произведение долей справившихся и не справившихся с заданиями; r pbis – точечно–бисериальный коэффициент.

16. Доверительный интервал:

η i= y i± tm,

где y i – тестовый балл; m – стандартная ошибка измерения; t – табличное значение распределения Стьюдента.

17. Формула Муавра (для кривой нормального распределения):

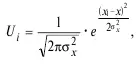
где U – высота кривой для каждого x i ; x – среднее арифметическое; σ 2 x– стандартное отклонение.

18. Коэффициент асимметрии:

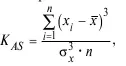
где x i – значение признака; x – среднее значение признака; n – число наблюдений; σ x– стандартное отклонение.

19. Эксцесс:

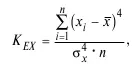
где x i – значение признака; x – среднее значение признака; n – число наблюдений, σ x– стандартное отклонение.

20. Однопараметрическая и двухпараметрическая модели Раша—Бирнбаума:

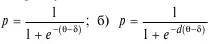
– вероятность выполнения тестируемым с уровнем подготовки q задания трудности δ; d – коэффициент дискриминативности.