Норберт Винер - Кибернетика или управление и связь в животном и машине

В любой группе характеров числа α( T ), соответствующие данному характеру f, распределены таким образом, [c.109]что это распределение не нарушается при умножении их всех на α( S ), каков бы ни был элемент S исходной группы. Иначе говоря, если есть какое-то разумное основание взять среднее от этих чисел, не затрагиваемое, когда группа преобразуется умножением каждого ее преобразования на одно фиксированное, то либо α( Т ) тождественно равно 1, либо наше среднее инвариантно относительно умножения на числа, отличные от 1, и потому должно равняться 0. Отсюда можно заключить, что среднее произведение характера на величину, с ним сопряженную (которая также является характером), будет равно 1, а среднее произведение характера на величину, сопряженную с другим характером, будет равно 0. Другими словами, если h ( x ) представлено как в (2.04), то

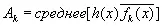(2.09)

Для группы поворотов по окружности это дает нам сразу, что если

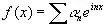(2.10)

то

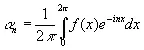(2.11)

Для сдвигов же по бесконечной прямой результат тесно связан с тем обстоятельством, что если в некотором подходящем смысле

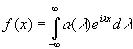(2.12)

то в определенном смысле

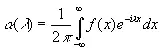(2.13)

Эти результаты изложены здесь очень грубо, без точной формулировки условий их справедливости. Более строгое изложение теории читатель может найти в работе, указанной в примечании [133]. [c.110]

Наряду с теорией линейных инвариантов группы, существует также общая теория ее метрических инвариантов. Последние представляют собой системы меры Лебега, не претерпевающие изменений, когда объекты, преобразуемые группой, переставляются операторами группы. В этой связи следует упомянуть интересную теорию групповой меры, которую дал Гаар [134]. Как мы видели, всякая группа сама есть собрание объектов, которые переставляются между собой при умножении на операторы данной группы. Поэтому она может иметь инвариантную меру. Гаар доказал, что некоторый довольно широкий класс групп имеет однозначно определенную инвариантную меру, задаваемую строением самой группы.

Наиболее важное применение теории метрических инвариантов группы преобразований состоит в обосновании взаимной заменимости фазовых и временных средних, которую, как мы видели выше, Гиббс тщетно пытался доказать. Это доказательство было выполнено на основе так называемой эргодической теории.

В обычных эргодических теоремах рассматривается ансамбль Е, меру которого можно принять за единицу, и этот ансамбль преобразуется в себя сохраняющим меру преобразованием Т или группой сохраняющих меру преобразований Т λ , где —∞< λ <���∞ и

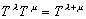(2.14)

Эргодическая теория имеет дело с комплексным функциями f ( х ) элементов х из Е. Во всех случаях f ( х ) считается измеримой по х, а если мы рассматриваем непрерывную группу преобразований, то f ( Т λх ) считается измеримой по х и λ вместе.

В эргодической теореме Купмена — фон Неймана о сходимости в среднем функция f ( х ) считается принадлежащей к классу L 2; это значит, что

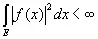(2.15)

Теорема утверждает, что [c.111]

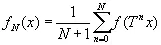(2.16)

или соответственно

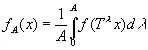(2.17)

сходится в среднем к пределу f *( х ) при N→∞ или соответственно при А→∞ в том смысле, что

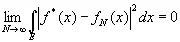(2.18)

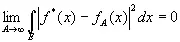(2.19)

В эргодической теореме Биркгоффа о сходимости «почти всюду» функция f ( х ) считается принадлежащей к классу L ; это значит, что

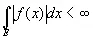(2.20)

Функции f N ( х ) и f A ( х ) определяются, как в (2.16) и (2.17). Теорема утверждает [135], что для всех значений х, за исключением множества нулевой меры, существуют пределы

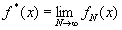(2.21)

и

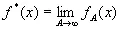(2.22)

Особенно интересен так называемый эргодический, или метрически транзитивный, случай, когда преобразование Т или множество преобразований Т λ не оставляет инвариантным ни одно множество точек х с мерой, отличной от 1 и 0. В таком случае множество значений (для обеих эргодических теорем), на которых f *( х ) пробегает заданный интервал, почти всегда есть 1 или 0. Это возможно только при том условии, что [c.112] f *( х ) почти всегда постоянна. Тогда f *( х ) почти всегда равна

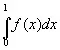(2.23)

Таким образом, в теореме Купмена мы получаем предел в среднем [136]

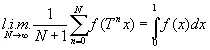(2.24)

а в теореме Биркгоффа

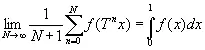(2.25)

за исключением множества значений х меры (или вероятности) 0. Аналогичные результаты имеют место в непрерывном случае. Это служит достаточным обоснованием производимой Гиббсом замены фазовых и временных средних.

Для случая, когда преобразование Т или группа преобразований Т λ не являются эргодическими, фон Нейман показал, что при очень общих условиях они могут быть сведены к эргодическим составляющим. Это значит, что, отбросив множество значений х нулевой меры, Е можно разбить на конечное или счетное множество классов Е n и континуум классов Е ( y ), таких, что на каждом Е n и Е ( y ) устанавливается мера, инвариантная при Т и Т λ . Все эти преобразования эргодические, и если S ( y ) — пересечение множества S с Е ( y ) , S n— пересечение множества S с Е n , то