Норберт Винер - Кибернетика или управление и связь в животном и машине

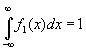(3.04)

Поэтому средний логарифм ширины области, расположенной под кривой f 1( x ), можно принять за некоторое среднее значение высоты логарифма обратной величины функции f 1( x ). Таким образом, разумной мерой [139]количества информации, связанного с кривой f 1( x ), может служить [140] [c.121]

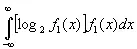(3.05)

Величина, которую мы здесь определяем как количество информации, противоположна по знаку величине, которую в аналогичных ситуациях обычно определяют как энтропию. Данное здесь определение не совпадает с определением Р.А. Фишера для статистических задач, хотя оно также является статистическим определением и может применяться в методах статистики вместо определения Фишера.

В частности, если f 1( x ) постоянна на интервале ( а, b ) и равна нулю вне этого интервала, то

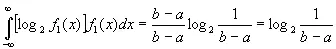(3.06)

Используя это выражение для сравнения информации о том, что некоторая точка находится в интервале (0, 1), с информацией о том, что она находится в интервале ( а , b ), получим как меру разности

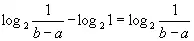(3.07)

Определение, данное нами для количества информации, пригодно также в том случае, когда вместо переменной х берется переменная, изменяющаяся в двух или более измерениях. В двумерном случае f 1( x , y ) есть такая функция, что

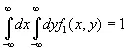(3.08)

и количество информации равно

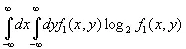(3.081)

Заметим, что если f 1( x, y ) имеет вид φ ( х ) ψ ( y ) и

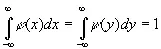, (3.082)

[c.122]

то

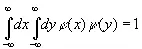(3.083)

и

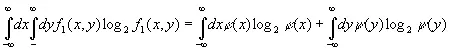(3.084)

т. е. количество информации от независимых источников есть величина аддитивная.

Интересной задачей является определение информации, получаемой при фиксации одной или нескольких переменных в какой-либо задаче. Например, положим, что переменная u заключена между х и x + dx с вероятностью

,

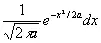а переменная v заключена между теми же двумя пределами с вероятностью

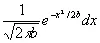
Сколько мы приобретаем информации об u , если знаем, что u + v = w ? В этом случае очевидно, что u = w — v , где w фиксировано. Мы полагаем, что априорные распределения переменных u и v независимы, тогда апостериорное распределение переменной u пропорционально величине

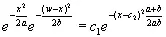, (3.09)

где c 1и c 2— константы. Обе они исчезают в окончательной формуле.

Приращение информации об u , когда мы знаем, что w таково, каким мы его задали заранее, равно

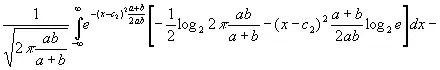[c.123]

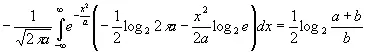(3.091)

Заметим, что выражение (3.091) положительно и не зависит от w. Оно равно половине логарифма от отношения суммы средних квадратов переменных u и v к среднему квадрату переменной v. Если v имеет лишь малую область изменения, то количество информации об u , которое дается знанием суммы u+v, велико и становится бесконечным, когда b приближается к нулю.

Мы можем истолковать этот результат следующим образом. Будем рассматривать u как сообщение, а v — как помеху. Тогда информация, переносимая точным сообщением в отсутствие помехи, бесконечна. Напротив, при наличии помехи это количество информации конечно и быстро приближается к нулю по мере увеличения силы помехи.

Мы сказали, что количество информации, будучи отрицательным логарифмом величины, которую можно рассматривать как вероятность, по существу есть некоторая отрицательная энтропия. Интересно отметить, что эта величина в среднем имеет свойства, которые мы приписываем энтропии.

Пусть φ ( х ) и ψ ( x ) — две плотности вероятностей, тогда

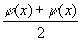
также есть плотность вероятности и

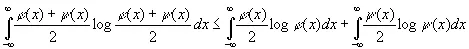(3.10)

Это вытекает из того, что

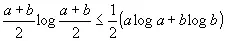(3.11)

Другими словами, перекрытие областей под φ ( х ) и ψ ( x ) уменьшает максимальную информацию, заключенную в сумме φ ( х )+ ψ ( x ). Если же φ ( х ) есть плотность [c.124]вероятности, обращающаяся в нуль вне ( а , b ), то интеграл

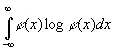(3.12)

имеет наименьшее значение, когда 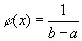на интервале ( а , b ) и φ ( х )=0 вне этого интервала. Это вытекает из того, что логарифмическая кривая выпукла вверх.

Как и следовало ожидать, процессы, ведущие к потере информации, весьма сходны с процессами, ведущими к росту энтропии. Они состоят в слиянии областей вероятностей, первоначально различных. Например, если мы заменяем распределение некоторой переменной распределением функции от нее, принимающей одинаковые значения при разных значениях аргумента, или в случае функции нескольких переменных позволяем некоторым из них свободно пробегать их естественную область изменения, мы теряем информацию. Никакая операция над сообщением не может в среднем увеличить информацию. Здесь мы имеем точное применение второго закона термодинамики к технике связи. Обратно, уточнение в среднем неопределенной ситуации приводит, как мы видели, большей частью к увеличению информации и никогда — к ее потере.