Норберт Винер - Кибернетика или управление и связь в животном и машине

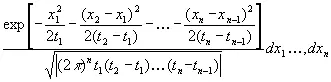. (3.18)

Исходя из создаваемой этим системы вероятностей, вполне однозначной, мы можем ввести на множестве путей, соответствующих различным возможным броуновым перемещениям, такой параметр α, лежащий между 0 и 1, что: 1) каждый путь будет функцией x ( t ,α), где х зависит от времени t и параметра распределения α и 2) вероятность данному пути находиться в данном множестве S будет равна мере множества значений α, соответствующих путях, находящимся в S . Поэтому почти все пути будут непрерывными и недифференцируемыми.

Весьма интересен вопрос об определении среднего значения произведения x ( t 1, α) … x ( t n, α) относительно α. Это среднее равно

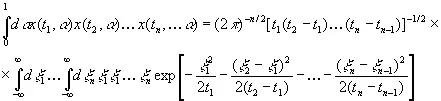(3.19)

при условии 0 ≤ t 1≤…≤ t n. Положим

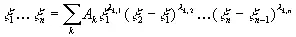(3.20)

[c.132]

где λ k,1+λ k,2+…+λ k,n = n .Тогда выражение (3.19) примет значение

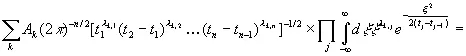
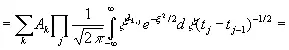
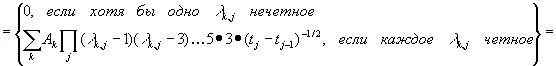
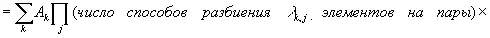
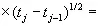
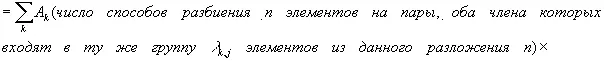
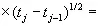
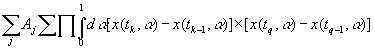. (3.21)

Здесь первая сумма берется по j ; вторая — по всем способам разбиения n элементов на пары в группах, включающих соответственно λ k,1, …, λ k,n элементов; произведение — по парам значений k и q, где λ k,1элементов среди выбранных t k и t q равны t 1, λ k,2элементов равны t 2и т. д. Отсюда сразу же следует

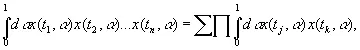(3.22)

[c.133]

где сумма берется по всем разбиениям величин t 1, …, t n на различные пары, произведение — по всем парам в каждом разбиении. Другими словами, если нам известны средние значения попарных произведений величин x ( t j , α), то нам известны и средние значения всех многочленов от этих величин и, следовательно, их полное статистическое распределение.

До сих пор мы рассматривали броуновы перемещения x ( t j ,α), в которых t положительно. Положив

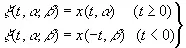, (3.23)

где α и β имеют независимые равномерные распределения в интервале (0, 1), получим распределение для ξ( t , α, β), где t пробегает всю бесконечную действительную ось. Существует хорошо известный математический прием отобразить квадрат на прямолинейный отрезок таким образом, что площадь преобразуется в длину. Надо лишь записать координаты квадрата в десятичной форме

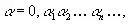
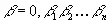(3.24)

и положить

,

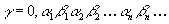и мы получим искомое отображение, являющееся взаимно однозначным почти для всех точек как прямолинейного отрезка, так и квадрата. Используя эту подстановку, введем

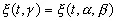. (3.25)

Теперь мы хотим определить в некотором подходящем смысле

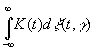(3.26)

Сразу приходит мысль определить указанное выражение как интеграл Стильтьеса [143], но это встречает [c.134]препятствие в том, что ξ представляет собой весьма нерегулярную функцию от t . Однако если К приближается достаточно быстро к нулю при t →± ∞ и является достаточно гладкой функцией, то разумно положить

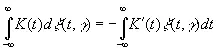(3.27)

При этих условиях мы формально получим

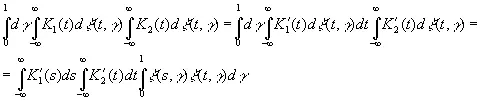(3.28)

Если теперь t и s имеют противоположные знаки, то

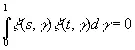(3.29)

а если они одного знака и |s|<| t |, то

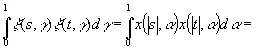
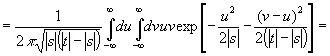
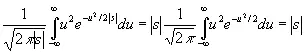(3.30)

[c.135]

Отсюда

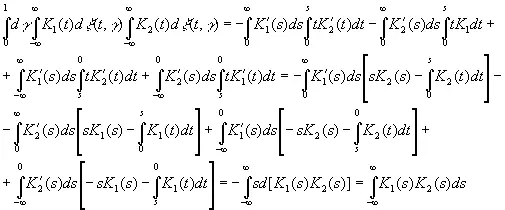(3.31)

В частности,

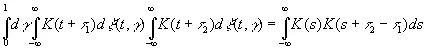(3.32)

Более того,

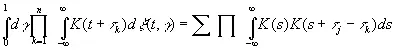(3.33)

[c.136]

где сумма берется по всем разбиениям величин τ 1, …, τ n на пары, а произведение — по парам в каждом разбиении. Выражение

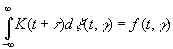(3.34)

изображает очень важный ансамбль временных рядов по переменной t, зависящих от некоторого параметра распределения γ. Доказанное нами равносильно утверждению, что все моменты и, следовательно, все статистические параметры этого распределения зависят от функции

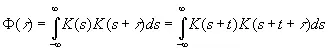(3.35)

представляющей собой известную в статистике автокорреляционную функцию со сдвигом τ. Таким образом, распределение функции f ( t , γ) имеет те же статистики, что и функция f ( t+t 1, γ); и действительно, можно доказать, что если