Норберт Винер - Кибернетика или управление и связь в животном и машине

то нахождение функции K ( s ) эквивалентно нахождению мнимой части log k (ω). Это задача неопределенная, если не наложить дальнейшего ограничения на k (ω). Налагаемое ограничение будет состоять в том, что log k (ω) должен быть аналитической функцией и иметь достаточно малую скорость роста относительно ω в верхней полуплоскости. Для выполнения этого условия предположим, что k (ω) и [ k (ω)] —1возрастают вдоль действительной оси алгебраически. Тогда [ F (ω)] 2будет четной и не более, чем логарифмически бесконечной функцией, и будет существовать главное значение Коши [146]для

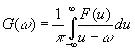(3.72)

Преобразование, определяемое выражением (3.72), называется преобразованием Гильберта; оно изменяет cos λω в sin λω и sin λω в —cos λω . Следовательно,

F (ω)+ iG (ω)

есть функция вида

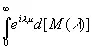(3.73)

и удовлетворяет требуемым условиям для log | k (ω)| в нижней полуплоскости.

Если теперь положить

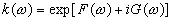, (3.74)

то можно показать, что при весьма общих условиях функция K ( s ), определяемая формулой (3.68), будет обращаться в нуль для всех отрицательных аргументов. Таким образом,

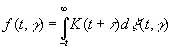(3.75)

[c.145]

С другой стороны, можно показать, что 1/ k (ω) записывается в виде

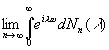, (3.76)

где значения N n определены подходящим образом, и что при этом можно получить

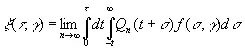(3.77)

Здесь значения Q n должны удовлетворять формальному условию

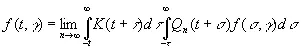(3.78)

В общем случае будем иметь

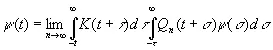, (3.79)

а если ввести по образцу соотношения (3.68)

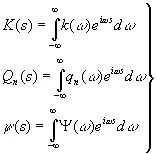, (3.80)

то

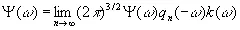. (3.81)

Следовательно,

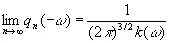. (3.82)

Этот вывод мы используем для того, чтобы получить оператор предсказания в форме, связанной не со временем, а с частотой. [c.146]

Таким образом, прошлое и настоящее функции ξ( t , γ), или точнее «дифференциала» d ξ( t , γ), определяют прошлое и настоящее функции f ( t , γ), и обратно.

Если теперь А >0, то

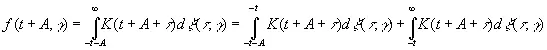(3.83)

Здесь первый член последнего выражения зависит от области изменения d ξ( τ , γ), в которой, зная лишь f (σ, γ) для σ≤ t , сказать ничего нельзя, и совершенно не зависит от второго члена. Его среднеквадратическое значение равно

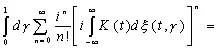, (3.84)

и эта формула дает все статистическое знание о нем. Можно показать, что первый член имеет гауссово распределение с этим среднеквадратическим значением. Последнее равно ошибке наилучшего возможного предсказания функции f ( t + A , γ).

Само же наилучшее возможное предсказание выражается вторым членом в (3.83):

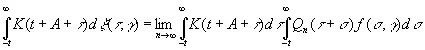. (3.85)

Если теперь положим

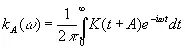(3.86)

[c.147]

и применим оператор (3.85) к e iωt, получив

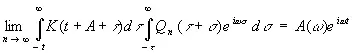, (3.87)

то найдем, подобно (3.81), что

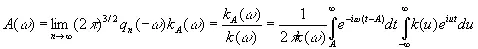(3.88)

Это и есть частотная форма наилучшего оператора предсказания.

Задача фильтрации в случае временных рядов типа (3.34) тесно связана с задачей предсказания. Пусть сумма сообщения и шума имеет вид

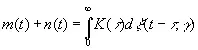, (3.89)

а сообщение имеет вид

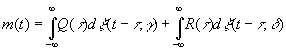, (3.90)

где γ и δ распределены независимо в интервале (0, 1). Тогда предсказуемая часть функции m ( t + a ), очевидно, равна

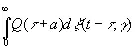, (3.901)

а среднеквадратическая ошибка предсказания равна

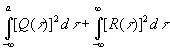. (3.902)

Допустим, кроме того, что нам известны следующие величины:

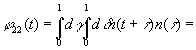[c.148]

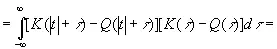
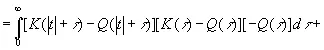
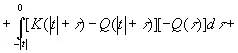
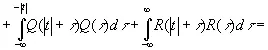
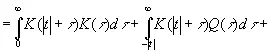
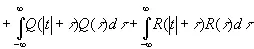(3.903)

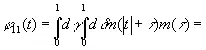
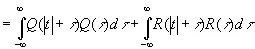(3.904)

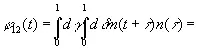
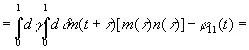
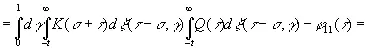
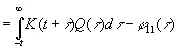(3.905)

[c.149]

Преобразование Фурье для этих величин соответственно равно

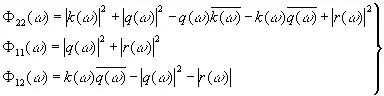(3.906)