Норберт Винер - Кибернетика или управление и связь в животном и машине

Кроме того, выше мы рассматривали простые временные ряды, в которых от времени зависит лишь одна числовая переменная. Существуют также многомерные временные ряды, где несколько таких переменных зависят все вместе от времени; именно многомерные ряды имеют наибольшее значение в экономических науках, метеорологии и т. п. Полная карта погоды Соединенных Штатов, составляемая ежедневно, есть такой временной ряд. В этом случае нам нужно одновременно выразить несколько функций через частоту, причем квадратические величины, такие, как выражение (3.35) или | k (ω)| 2в рассуждениях после формулы (3.70), заменяются множествами пар величин, т. е. матрицами . Задача определения функции k (ω) через | k (ω)| 2с выполнением некоторых добавочных условий в комплексной плоскости становится теперь гораздо труднее, особенно ввиду того, что умножение матриц не является перестановочной операцией. Тем не менее задачи, относящиеся к этой многомерной теории, были решены, по крайней мере частично, Крейном и автором.

Многомерная теория представляет собой усложнение предыдущей теории. Существует, кроме того, другая близкая теория, которая является ее упрощением. Эта теория предсказания, фильтрации и количества информации в дискретных временных рядах. Такой ряд [c.154]представляет собой последовательность функций f n (α) параметра α, где n пробегает все целочисленные значения от —∞ до ∞. Величина α, как и раньше, служит параметром распределения, и можно по-прежнему считать, что этот параметр изменяется равномерно в интервале (0, 1). Говорят, что временной ряд находится в статистическом равновесии, если замена n на n + v ( v — целое число) равносильна сохраняющему меру преобразованию в себя интервала (0, 1), пробегаемого параметром α.

Теория дискретных временных рядов во многих отношениях проще теории непрерывных рядов. Гораздо легче, например, свести их к последовательности независимых выборов. Каждый член (в случае перемешивания) можно представить как комбинацию предшествующих членов с некоторой величиной, не зависящей от всех предшествующих членов и равномерно распределенной в интервале (0, 1), и последовательность этих независимых коэффициентов взять вместо броунова движения, столь важного для непрерывных рядов.

Если f n (α) — временной ряд, находящийся в статистическом равновесии и метрически транзитивный, то его коэффициент автокорреляции будет равен

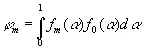. (3.923)

и мы будем иметь

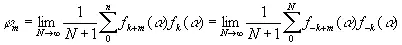(3.924)

почти для всех α. Положим

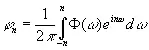, (3.925)

или

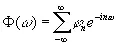(3.926)

[c.155]

Пусть

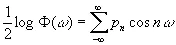, (3.927)

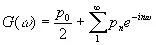(3.928)

и

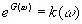. (3.929)

Тогда при очень общих условиях k (ω) будет граничным значением на единичном круге для функции без нулей и особых точек внутри единичного круга; ω является здесь углом. Отсюда

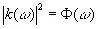(3.930)

Если теперь за наилучшее линейное предсказание функции f n (α) с опережением v принимается

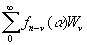, (3.931)

то

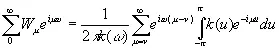. (3.932)

Это выражение аналогично выражению (3.88). Заметим, что если положить

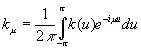, (3.933)

то

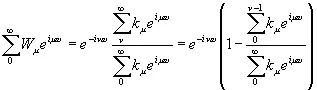(3.934)

[c.156]

Из нашего способа образования k (ω) видно, что для весьма широкого класса случаев мы вправе положить

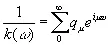. (3.935)

Тогда уравнение (3.934) принимает вид

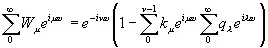. (3.936)

В частности, при v =1

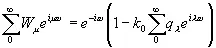, (3.937)

или

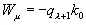(3.938)

Таким образом, при предсказании на один шаг вперед наилучшим значением для f n +1(α) будет

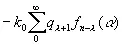; (3.939)

последовательным же предсказанием по шагам мы можем решить всю задачу линейного предсказания для дискретных временных рядов. Как и в непрерывном случае, это будет наилучшим возможным предсказанием относительно любых методов, если

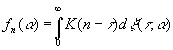. (3.940)

Переход от непрерывного случая к дискретному в задаче фильтрации совершается примерно таким же путем. Формула (3.913) для частотной характеристики наилучшего фильтра принимает вид

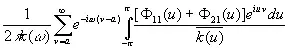, (3.941)

где все члены имеют тот же смысл, что и в непрерывном случае, за исключением того, что все интегралы по ω и u [c.157]имеют пределы от —π до π, а не от —∞ до ∞ и вместо интегралов по t берутся дискретные суммы по v . Фильтры для дискретных временных рядов представляют собой обычно не столько физически осуществимые устройства для применения в электрической схеме, сколько математические процедуры, позволяющие статистикам получать наилучшие результаты со статистически несовершенными данными.

Наконец, скорость передачи информации дискретным временным рядом вида

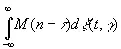, (3.942)

при наличии шума

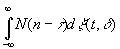, (3.943)